Introduction to Square Roots
In the exponents unit we took a close look at exponents and powers. You may want to review the lesson on exponents before starting this lesson.
Let's get started.
Another term for raising a number to the 2nd power is "squaring a number". For example:
22 = 4. This can be read as 2 "squared" equals 4. This means that 2 x 2 = 4.
32 = 9. This can be read as 3 "squared" equals 9. This means that 3 x 3 = 9.
42 = 16. This can be read as 4 "squared" equals 16. This means that 4 x 4 = 16.
As you've probably discovered in Math, there is always an "opposite" operation. So, can you guess the opposite operation for "squaring" a number?
You've got it - taking the "square root" is the opposite of squaring a number!
Let's take a look at the symbols.
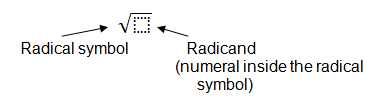
Before we dig in, let's look at some familiar vocabulary. The symbol used for identifying roots is called the radical sign.
The number inside the radical sign is called the radicand.
When you start Algebra 2, you will also learn that if you are working with cube roots, or fourth roots..., there will be another number called the index. We'll worry about the index later.
Take a look at the diagram below to further explain these definitions.
Take a look at the chart below for a list of the most common square roots.
Tip
It is a common mistake to identify the square root of 4 as 2 and -2.
Typically when working with square roots, we only want to identify the "principal square root" which is the positive answer only.
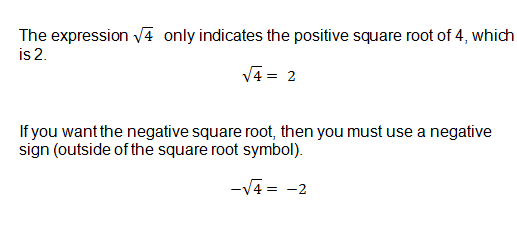
Why did I stress that if you want a negative square root, that the negative sign must be outside of the radical sign?
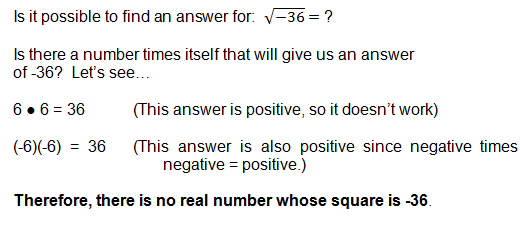
Wow! We've covered a lot in this lesson, but let's look at one more example.
What Happens When You Take the Square Root of a Fraction?
When you take the square root of a fraction, simply take the square root of the numerator and the square root of the denominator. The answer remains a fraction. Take a look at the following examples.
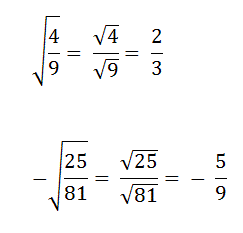
Wow! We've accomplished a lot, and there's a lot more to learn. But, we'll take it one step at a time, and soon you'll have a solid understanding of quadratics.
Now, you are ready to start our first lesson on solving quadratic equations.
Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.
Need Help? Try This Online Calculator!
Affiliate Products...
On this site, I recommend only one product that I use and love and that is Mathway If you make a purchase on this site, I may receive a small commission at no cost to you.
Comments
We would love to hear what you have to say about this page!