Solving an Absolute Value Equation:  Lesson 1

Before we get into solving absolute value equations, let's first quickly review what the term "absolute value" means.

Absolute Value

The absolute value of a number is its distance from 0 on the number line.

Remember: Distance can never be negative; therefore, the absolute value of a number is always positive.

Absolute value is indicated by the absolute value bars: |x|


Examples:

| -5| = 5       (-5 is five units away from 0 on the number line).

|5| = 5        (5 is also five units away from 0 on the number line).

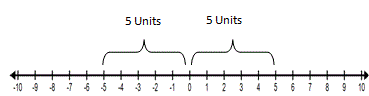
More Examples:

|-10| = 10     and     |10| = 10

|-55| = 55     and     |55| = 55


Did you notice how in the above examples, the answers of 10 and 55 were the same for two different expressions?

By this I mean that:   |-10| = 10      and        |10| = 10.

Two different expressions have an answer of 10 because the absolute value of a number is always positive.


So, think about this...

Evaluate the expression:

|x| = 4    This means: What value can we substitute for x to get an answer of 4?

**You might automatically say: x = 4    because |4| = 4

Yes, you are correct! However, this is not the only answer. You will have two answers for this equation because:

Isn't |-4| = 4 ?

So, this answer is x = 4 or -4.


This concept will play an important role as we solve absolute value equations. Pay careful attention because many of your equations will have two answers.


Example 1: Solving an Absolute Value Equation

This example shows how to solve the absolute value equation, "the absolute value of x minus 9 is equal to 20.
Checking the absolute value equation


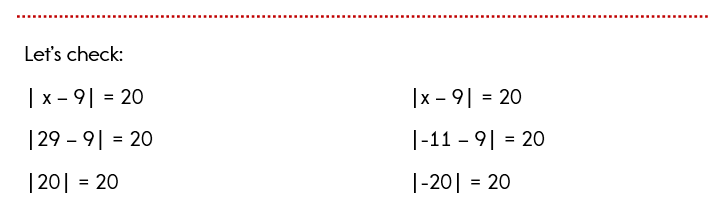
You must remember that when you are solving an absolute value equation, you will want to write two separate equations to solve. This is because the value inside of the absolute value bars can be positive or negative to result in the same answer.

Let's take a look at another similar example just to clarify any problems or questions.


Example 2 - More Absolute Value Equations

This example shows how to solve the absolute value of x plus 14 equal 5.


I hope that you are feeling more comfortable with absolute value equations. There is a time when you may not have a solution. Yes, there always has to be tricks, just to keep you on your toes.

When working with absolute value, think about what might not be possible...


Example 3 - No Solution

What would you substitute for x in the following equations to make the equation true?

|x| = -3


Can you think of an answer for x? Probably not, because there is no answer. There is no way that you can take the absolute value of a number and have a negative answer.

Therefore, if you come across an equation, such as the following:

|x - 5| = -4

You can stop right there and write the empty set as your answer.

You do not have to write two equations and solve, because there are no real answers to this equation.

Do not write 0 as your answer. The answer is the empty set and is written as follows:


empty set

Quick Recap:

  • For most absolute value equations, you will write two different equations to solve. The value inside of the absolute value can be positive or negative.

  • If the answer to an absolute value equation is negative, then the answer is the empty set. No absolute value can be a negative number.


  1. Home
    2. >
  2. Solving Equations
    3. >
  3. Absolute Value Equations



Comments

We would love to hear what you have to say about this page!

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.