Do You Need Help Interpreting an Area Formula?
Area is the number of square units inside of a shape. We typically find the area of a shape that is two dimensional (like a floor, or a piece of carpet, or a piece of land).
Since the area is measuring the number of square units inside of the shape, the units must be written as squared units (ex: cm2).
Many of the area formulas require you to know the height of the shape.
The height of the shape is always the distance from the top of the shape to the bottom. The height must be a straight, vertical line.
Keep this page handy as you study formulas and solve real world problems throughout your algebra studies!
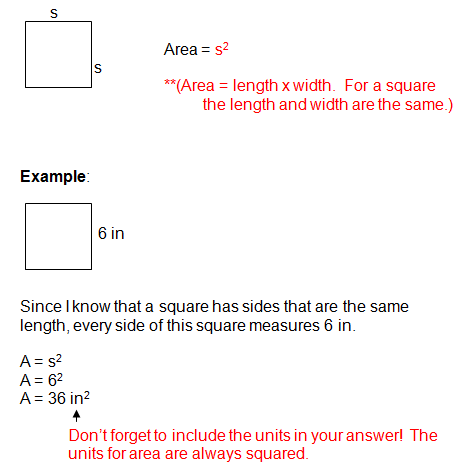
Area of a Square
A square has 4 sides that are all exactly the same size. Therefore, finding the area is pretty easy! Since the area of a square or rectangle is length x width, we can just square the length of the side! Take a look!
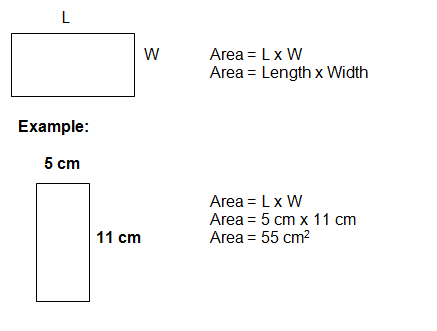
Area of a Rectangle
A rectangle is a 4 sided figure with two pairs of parallel lines. Each set of parallel lines has the same length. To find the area of a rectangle we are going to multiply the length x the width.
Area of a Parallelogram
A parallelogram is another 4 sided figure with two pairs of parallel lines. To find the area of a parallelogram, we will multiply the base x the height. Let's look at the formula and example.
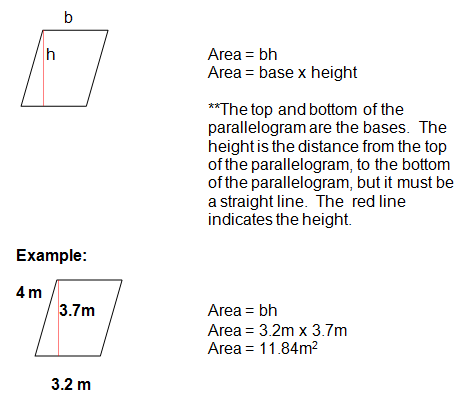
Notice that we did not use the measurement of 4m. 4m did not represent the base or the height, therefore, it was not needed in our calculation.
Area of a Trapezoid
A trapezoid is a 4 sided figure formed by one pair of parallel sides. This area formula is a little more complicated. Study the example carefully!
Take note that the bases of a trapezoid are always the parallel lines.
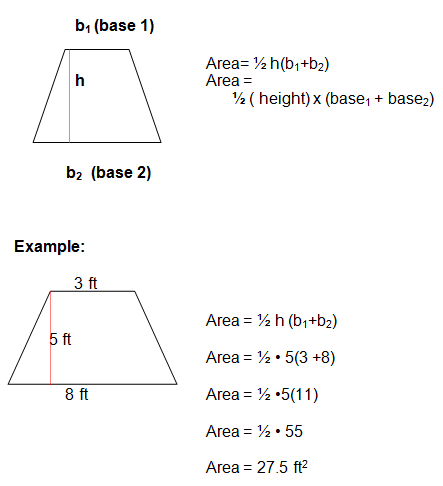
Area of a Triangle
A triangle is a 3 sided figure. There are several different types of triangles. You must be careful when trying to locate the height of the triangle. Remember the height of the shape must be a straight, vertical line.
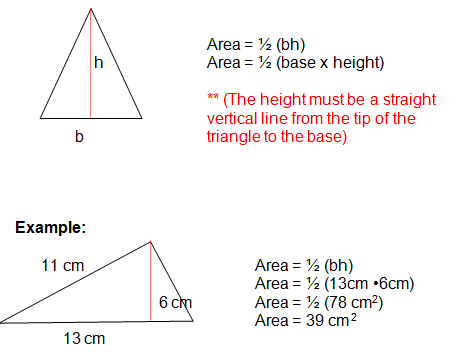
Again, notice that we did not need to use the measurement of 11cm. 11cm did not represent the base of the triangle, nor did it represent the height.
** You will not always need to use every measurement that is given in the problem.
Area of a Circle
A circle, of course, has no straight lines. We use pi (3.14) when we calculate the area of a circle.

What Would Happen if We Were Given the Diameter of the Circle and Asked to Find the Area?
f you are given the diameter of a circle (which is the distance
across the circle - through the center), then you would divide the
diameter in half. One-half of the diameter = the radius.
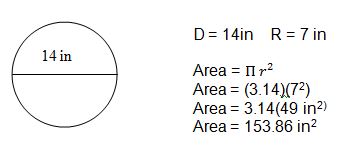
Don't forget that the area is a measurement of the inside space of a two dimensional figure. We are measuring how many "square units" fit on the inside.
I hope that these formulas have helped you to solve your algebra problems. Good luck!

Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.





Comments
We would love to hear what you have to say about this page!