Multiplying Binomials:
Products That Result in the Difference of Two Squares
Another frequently occuring problem in Algebra is multiplying two binomials that differ only in the sign between their terms. An example would be:
(x - 4)(x + 4)
Notice that the only difference in the two binomials is the addition/subtraction sign between the terms.
We will solve this problem using the FOIL in Example 1. Then we will look at a special rule that can be applied to make this problem much easier to multiply.
Example 1: Using the FOIL Method

Did you notice how the middle terms added up to 0? This will happen every time you multiply two binomials whose only difference is the sign between the terms (+ and -).
The rule for multiplying this kind of binomial is:
Difference of Two Squares
When multiplying binomials whose only difference is the sign between the two terms, square the first term, square the second term, and subtract.
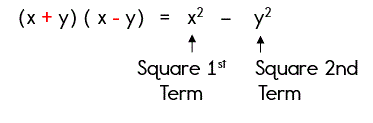
Let's take a look at the first example and apply this new rule.
Example 1: Using our Special Rule

Difference of Two Squares
The expression x2 - y2 is called the difference of two squares.
Let's take a look at one more example using our special rule.
Example 2: Difference of Two Squares
Yes, I know what you are thinking... it is much easier to use the special rule.
However, you need to remember that this is a "special case" and this rule ONLY works when the binomials only differ by the plus and minus sign between the terms.
Great Job! Now, you are ready to start factoring polynomials.

Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.
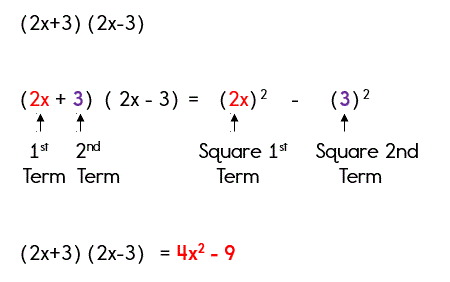





Comments
We would love to hear what you have to say about this page!