Calculating Slope
The Key to Graphing Equations

What do you think of when you hear the term, slope? Do you think of a skier, skiing down a large mountain?

Or, maybe you think of the sliding board at the playground.

Whatever you are thinking, it's probably something that's on an incline! When we study slope in Algebra we are going to study the incline and other characteristics of a line on a graph.

Slope is a very important concept to understand in Algebra. Therefore, I've created three different lessons to help you gain a full understanding.

We will start here with defining and calculating slope by analyzing a graph. Then we will move on to graphing slope and finally to using slope intercept form to create your graph.

Start here from the beginning, or move onto the concept of slope that you need help with!


What is Slope in Algebra?

Slope is used very often in Mathematics. It can be used to actually find how steep a particular line is, or it can be used to show how much something has changed over time. We calculate slope by using the following definition.

In Algebra, slope is defined as the rise over the run. This is written as a fraction like this:

Slope = rise over run

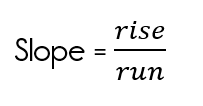
Rules for Calculating the Slope of  Line

  • Find two points on the line.

  • Count the rise (How many units do you count up or down to get from one point to the next?) Record this number as your numerator.

  • Count the run (How many units do you count left or right to get to the point?) Record this number as your denominator.

  • Simplify your fraction if possible.


Important Note:

  • If you count up or right your number is positive.

  • If you count down or left your number is negative.


There are two examples below. You can watch how I calculate slope in the video lesson, or you can skip the video and check out examples 1 and 2 below.


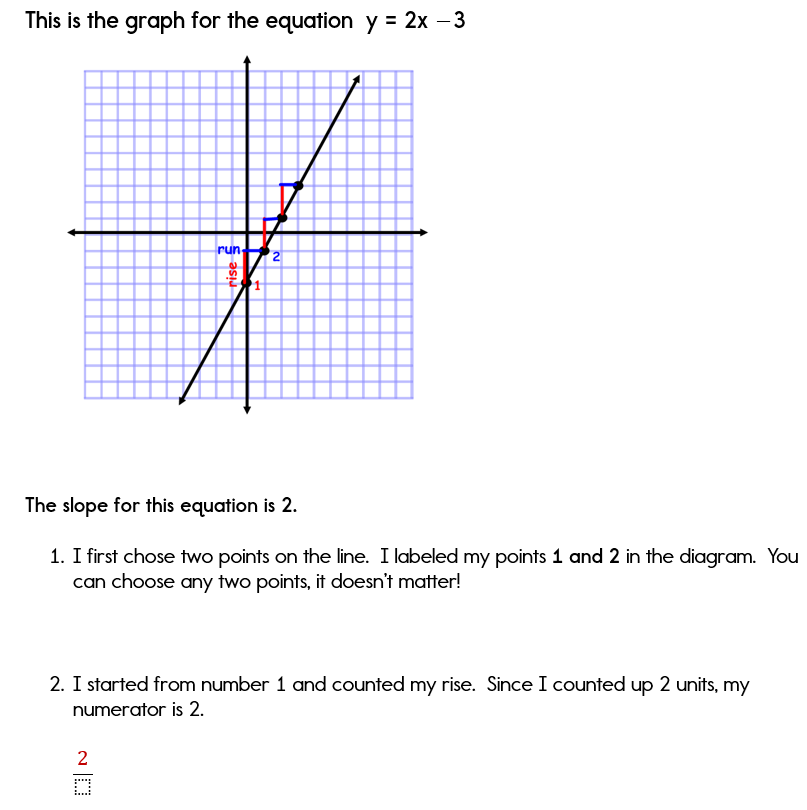
Example 1: Calculating Slope

Calculating slope
Calculating slope


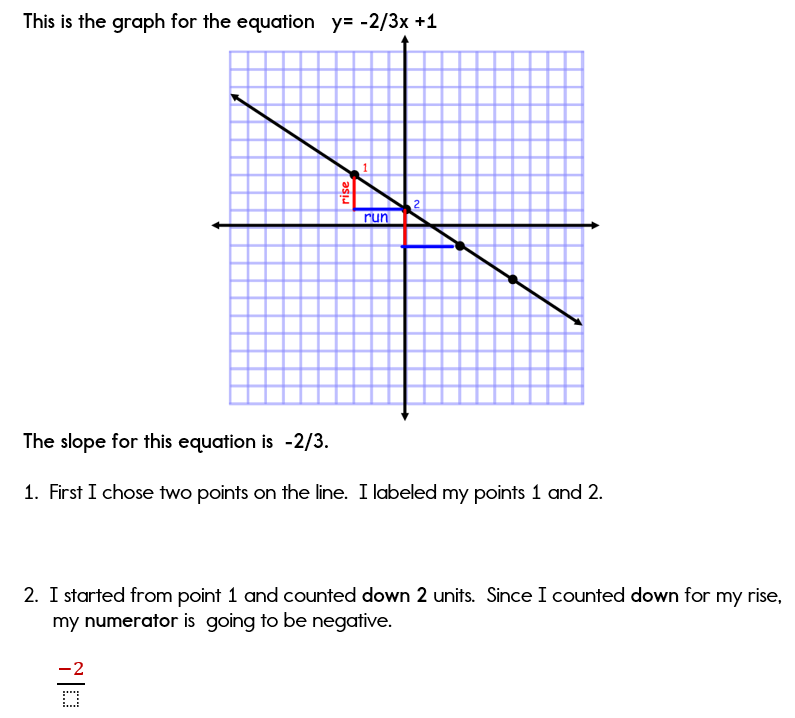
Let's take a look at another example where the slope is a fraction.



Example 2: Calculating Slope

Calculating slope example
Calculating slope example continued

Just Remember:

Slope is a fraction: rise/run. Calculate your rise and then your run!

If your rise is downhill it is negative. If your run is to the left it is also negative!

You can choose any two points on the line to calculate your slope! The slope is constant throughout the whole line.



  1. Home
    2. >
  2. Graphing Equations
    3. >
  3. Calculating Slope



Comments

We would love to hear what you have to say about this page!

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.