What is a Compound Inequality?

As your study of inequalities progresses, you will be introduced to a compound inequality. These inequalities can be a little tricky, so let's first take a look at the definition.

Do you notice how each of the problems above consist of two inequalities?

Let's begin by focusing on "AND" inequalities.

"And" Compound Inequalities

---

The solution to an "And" inequality is the intersection of the solution sets for two different inequalities. It's best explained through looking at a graph. Take a look with me...

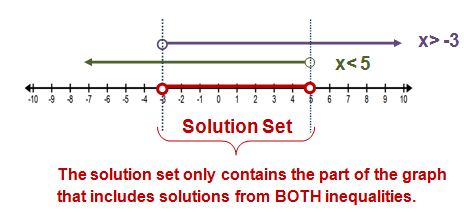
Do you notice how the solution set for the compound inequality only includes the solution sets that intersect or overlap on the graph? This is the most important rule to remember for "AND" compound inequalities.

One other thing I'd like to point out is that many "And" compound inequalities are not actually written with the word "and".

For example, this inequality shown above is most likely to be written as:

-3 < x < 5

This can be read as " x is greater than -3 and x is less than 5". Do you notice how you say the word "and", but you don't use the word "and" when actually writing the compound inequality? Here's why it can be read like this:

This one inequality can be broken into 2 different inequalities:

So, through this brief introduction, you should understand that there are two types of compound inequalities, "And" inequalities and "Or" inequalities.

If the inequality is an "And" compound inequality, then the solution is the intersection of the solution sets for both inequalities. You may not see the word "and" in the original inequality, but when you read the inequality aloud, you will say the word "and".

---

Now let's move on to compound inequalities that use the word "OR".

"OR" Compound Inequalities

---

The nice thing about "Or" inequalities is that you will always see the word "or" in the problem. This makes it easier to distinguish between the two types of inequalities.

The solution to a compound inequality containing the word "or" is the union of the solution sets. This means that the solution sets will not overlap or intersect. We will be uniting the solution sets instead. Let's take a look at a graph for a better picture.

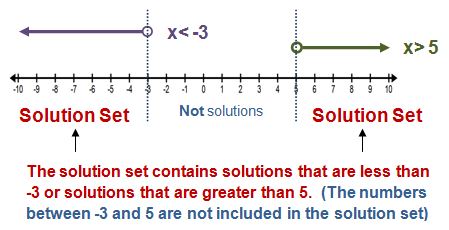
The final graph for this compound inequality would look exactly as it is shown:

Did you notice how the solution set for each individual inequality did not overlap at all? Therefore, our solution set for the compound inequality must include both sets of solutions. In a sense we are uniting these two answers in order to include both.

---

And lastly, here's a little vocabulary for you to add to your list:

Hopefully by now you better understand the difference in the two types of compound inequalities and you have an idea of what the graph will look like for each type of compound inequality.

In order to better understand these types of inequalities, you will want to study the following lessons:

• Solving and graphing conjunction compound inequalities.


• Solving and graphing disjunction compound inequalities.

1. Home
>
2. Inequalities
>
3. Compound Inequalities

---

---

Copyright © 2009-2020   |   Karin Hutchinson   |   ALL RIGHTS RESERVED.