Use These Examples of Probability To Guide You Through Calculating the Probability of Simple Events

Probability is the chance or likelihood that an event will happen.

It is the ratio of the number of ways an event can occur to the number of possible outcomes. We'll use the following model to help calculate the probability of simple events.


As you can see, with this formula, we will write the probability of an event as a fraction.

The numerator (in red) is the number of chances and the denominator (in blue) is the set of all possible outcomes. This is also known as the sample space.

Let's take a look at a few examples of probability.


Example 1- Probability Using a Die

Given a standard die, determine the probability for the following events when rolling the die one time:

P(5)

P(even number)

P(7)

Before we start the solution, please take note that:

P(5) means the probability of rolling a 5

When you see P(  ) this means to find the probability of whatever is indicated inside of the parenthesis.

Solutions:

Let’s first identify the sample space.  The sample space then becomes the denominator in our fraction when calculating probability.

 

Sample Space:      6      We are using a standard die.  A standard die has 6 sides and contains the numbers 1-6. 

Therefore, our sample space is 6 because there are 6 total outcomes that could occur when we roll the die.  The 6 outcomes are: 1, 2, 3, 4, 5, 6


Special Note:

Always simplify your fraction if possible!


Now let's take a look at a probability situation that involves marbles.


Example 2 - Probability with Marbles

There are 4 blue marbles, 5 red marbles, 1 green marble, and 2 black marbles in a bag.  Suppose you select one marble at random.  Find each probability.

P(black)

P(blue)

P(blue or black)

P(not green)

P(not purple)


Hopefully these two examples have helped you to apply the formula in order to calculate the probability for any simple event.

Now, it's your turn to try! Check out the spinner in the practice problem below.


Practice Problem


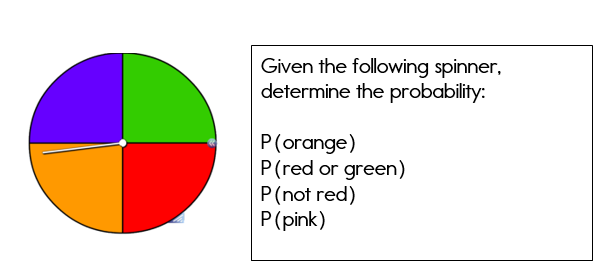
Solutions


Great Job! You've got the basics, now you are ready to move on to the next lesson on Tree Diagrams & The Fundamental Counting Principle.



  1. Home
    2. >
  2. Probability
    3. >
  3. Simple Probability



Comments

We would love to hear what you have to say about this page!

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.