Factoring a Trinomial with a Lead Coefficient Greater Than One

So, you are factoring trinomials and when you get to a trinomial that has a lead coefficient greater than 1, you start to panic. Does that sound familiar?

Confused already because you aren't sure what a lead coefficient greater than 1 means?"

Lead coefficient greater than 1

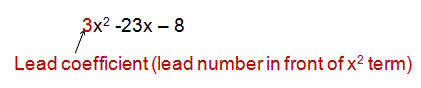
Yes, you've probably discovered that these trinomials are a little more difficult to factor. But, no worries, if you can factor by grouping, then I am going to show you a very simple, easy way to factor these trinomials.


Example 1: Factoring a Trinomial

Factor the trinomial: 3x2 - 24x - 8.

Our first step is to "set up" the problem so that we can factor this trinomial by grouping. In order to factor by grouping, we will need to rewrite the trinomial with four terms. Pay close attention to how this is done.

We first need to identify two "Magic Numbers". We will find these numbers by using the following method:

Did you notice how we found the two "magic numbers" and they helped us to rewrite the trinomials with four terms. I hope that you also noticed that the new polynomial with four terms is still equivalent to the original trinomials. When you combine like terms, we end up with the same middle term that is contained in the original trinomial.

Once you have a new set-up with four terms, you can use the grouping method to continue factoring this trinomial. I find it to be much easier than the guess and check method and I hope you do too!

Now we will take a look at one more example. In this example take note of the my very first step.



Example 2: Factoring with a Lead Coefficient Greater Than One

Factor: 12x2+14x + 4

I notice that this trinomial has larger numbers and the first thing I'm going to do it see if there is a greatest common factor (GCF) that I can factor out of this trinomial. This will allow me to work with smaller numbers.


Factoring a trinomial with a lead coefficient greater than 1.

I hope that these two examples help you to factor these tough trinomials. If you had trouble, you may want to go back and check out the factoring by grouping lesson as that is a prerequisite to this lesson.

Wishing you all the best!


  1. Home
    2. >
  2. Polynomials
    3. >
  3. Factoring Trinomials



Comments

We would love to hear what you have to say about this page!

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.