Factoring Trinomials

Factoring trinomials is probably the most common type of factoring in Algebra. In this lesson, we will factor trinomials that have a lead coefficient of 1.


To begin this lesson, it is important for you to understand the process of multiplying binomials using the FOIL method. Please be sure to review that lesson before starting this lesson.

The diagram below outlines the product of multiplying two binomials.

It's important to understand how we reach the trinomial because in this lesson we are going to work backwards to form the factors or two binomials.


Result of Multiplying Two Binomials

Did you notice how we added the two last terms of each binomial (3 & 5) to get the middle term and we multiplied the same two last terms (3 & 5) in order to get the last term of the trinomial?


Ok, now let's work backwards. You will be given the trinomial and in order to factor the trinomial, you will need to work backwards to find the two binomials. Let's look at an example.


Example 1: Factoring Trinomials

Factoring Trinomials


Just 3 easy steps to factoring trinomials. Let's take a look at another example. This example is a little more difficult because we will be working with negative and positive numbers.


Example 2: More Factoring

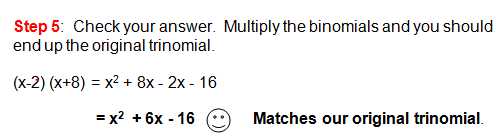
Tip:

When you have a trinomial with a minus sign, pay careful attention to your positive and negative numbers.

In the example above, 8 and -2 are the numbers that we needed to complete our binomials; however, -8 and 2 would not have worked!


I know that factoring trinomials is tough, so let's look at one more example. Again, this trinomial will contain a minus sign, so pay careful attention to the positive and negative numbers that you choose.


Example 3: Factoring Trinomials

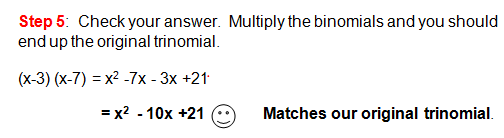
Hopefully you feel a little better now about factoring trinomials.  You may come across a trinomial that does not have a lead coefficient of 1.  In that case, check out our lesson on factoring trinomials with a lead coefficient greater than 1.


  1. Home
    2. >
  2. Polynomials
    3. >
  3. Factoring Trinomials



Comments

We would love to hear what you have to say about this page!

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.