Multiplying Binomials
Using the Foil Method

Multiplying polynomials becomes a little trickier when you multiply two binomials. We are still going to use the distributive property, but many students refer to the acronym, FOIL in order to remember the steps for multiplying binomials.


I am actually going to show you two ways to multiply binomials. The first way is thinking of it as another way to use the distributive property. The second way will be to use the FOIL Method. Let's take a look at the following examples.

Example 1: Using the Distributive Property

We will use the distributive property to multiply the following binomials:

(3x - 4)(2x +1)


Now, that seems like a lot of work doesn't it? That is the process for multiplying binomials, but eventually you'll be able to complete this process without writing out each step of the distributive property. I wrote it out, in hopes that you will understand the process. You will be able to do a lot of those steps mentally!

One way to help you remember the steps to perform mentally is to remember the acronym, FOIL. If you compare each step in the first example, to the steps used in example 2 with the foil method, you will find that they are pretty much the same. Let's take a look!


FOIL stands for:


Let's see how we can use FOIL to multiply two binomials.


Example 2: Using Foil

Let's take a look at the same problem demonstrated in Example 1 and see how FOIL can help us to remember all the steps in multiplying binomials.


We will multiply the same two binomials:

(3x - 4)(2x +1)



As you can see, when using FOIL ,we first distributed the 3x throughout the quantity      (2x +1). Then we distributed the -4 throughout the quantity (2x + 1). So, you can think of it as distributing one binomial throughout the other or you can remember FOIL to perform the same steps!


Let's look at another example using FOIL.


Example 3: Using the FOIL Method

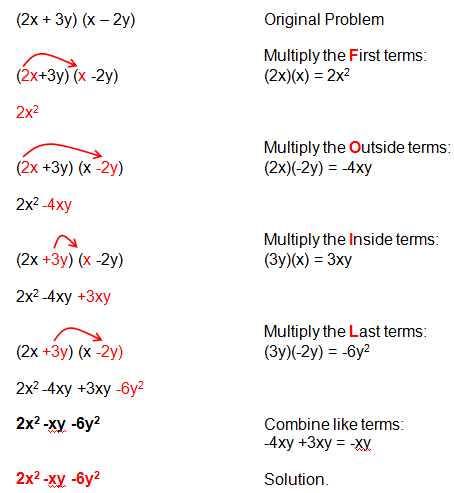
TIP

There is one thing that you need to remember with FOIL! It only works when you are multiplying two binomials.

This is not the only method used when multiplying polynomials and it doesn't work for all polynomials. It ONLY works with two binomials!


Are you ready to practice?


Practice Problems

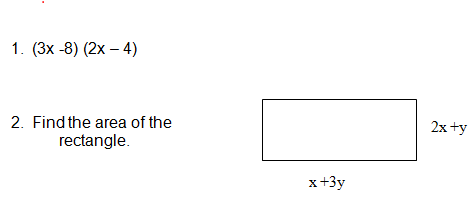
Solutions

Problem 1:


Problem 2:


Great Job! In the next lesson, we will take a look at a few "special cases" when multiplying binomials!

  1. Home
    2. >
  2. Polynomials
    3. >
  3. Using FOIL



Comments

We would love to hear what you have to say about this page!

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.