Understanding Integers

Definition: The term integer represents all natural numbers and their opposites. Fractions and decimals are not integers.

Integers can be shown as a set of numbers, as in this example:



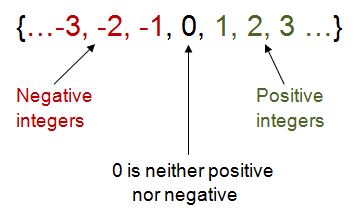
If a number is greater than 0, it is called a positive integer. No sign is needed to indicate a positive integer.

Look at the number line above. All numbers to the right of 0 are positive.

Examples: 4, 8, and 15 are positive numbers.

The arrows on the end of the number line indicate that the number line goes on until infinity (forever).

Positive integers are pretty easy at this point, because you've been working with them since you started school!

So... let's move on.

Tip

For every positive integer there is a negative integer. They are called opposites.

Examples:

5 and -5 are opposites

20 and -20 are opposites


Negative Integers

Negative Integers are less than 0 (or to the left of 0 on the number line.) If a number is negative, there will be a negative (-) symbol in front of the number.

Example: -2, -6, and -20 are negative integers



The trickiest thing to understand about negative numbers is that the farther away from 0, the smaller the number.

Example: -5 is less than -2.

(Think about this - if you OWE someone $5, then you will have less money after paying, than if you only OWED $2.)


Other Examples: -10 is less than -8.

Or... you could say that -3 is greater than -19.



Another Tip

When ordering negative numbers:

The closer the negative number is to 0, the larger it is.


Just remember, that when you are referring to integers, integers must be positive or negative whole numbers. A fraction or decimal is never considered an integer.

Positive integers are greater than zero, and negative integers are less than zero. Zero is an integer, but it is neither positive nor negative.



  1. Home
    2. >
  2. Integers
    3. >
  3. What Are Integers?



Comments

We would love to hear what you have to say about this page!

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.