Polynomials
Welcome to the Algebra 1 Polynomials Unit!
This unit is a brief introduction to the world of Polynomials. We will add, subtract, multiply, and even start factoring polynomials.
Click on the lesson below that interests you, or follow the lessons in order for a complete study of the unit.
Polynomials Unit
- Introduction to Polynomials (Definitions)
- Adding Polynomials
- Subtracting Polynomials
- Multiplying Polynomials
- Using the FOIL Method to Multiply Binomials
- Squaring a Binomial - Using a Special Rule
- Difference of Two Squares - "Special Binomials" Using a Special Rule
- Factoring Polynomials Using the Greatest Common Factor (GCF)
- Factoring Polynomials by Grouping
- Factoring Trinomials
- Factoring Trinomials with A Lead Coefficient Greater Than One
Need Additional Help?
As you study this unit, if you find that you need more help, please visit the Algebra Class E-courses. You will find many examples on video, and a lot of practice problems with step-by-step answer keys.
Introduction to Polynomials
So, what is a Polynomial? This is definitely not a word that we hear everyday.
A Polynomial is a finite sum of terms. This includes subtraction as well, since subtraction can be written in terms of addition. Let's take a look at a couple of examples and this will make more sense.
Examples of Polynomials
2x2 + 3x - 5
2x2y2 + 3xy - 5xy2
5x + 3y +6x +2y
As you can see from the examples above, we are simply adding (or subtracting) two or more terms together.
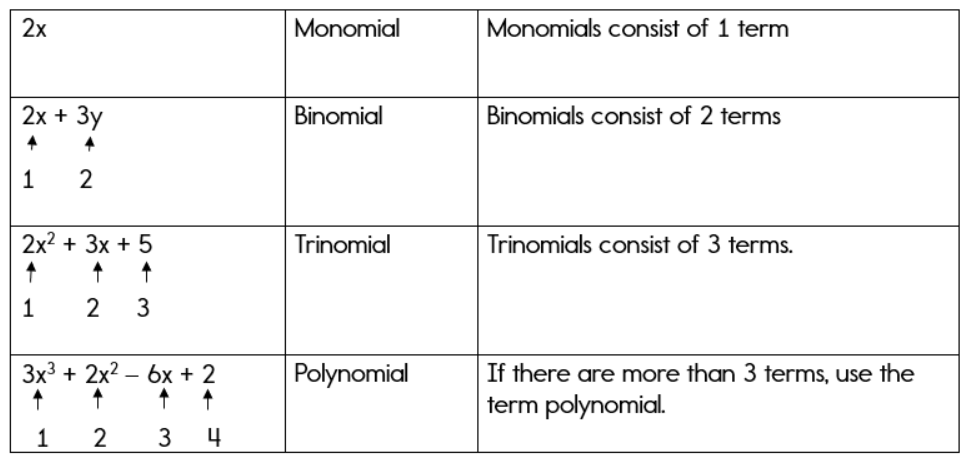
Polynomials can also be classified according to the number of terms. Let's take a look!
REMEMBER: Terms are separated by a plus sign or a minus sign.
Let's take a look at one more definition! The degree of a polynomial with one variable is the highest power to which the variable is raised. Take a look!
Degree of Polynomials
Polynomials in one variable should be written in order of decreasing powers. If this is the case, the first term is called the lead coefficient. The exponent of this first term defines the degree of the polynomial.
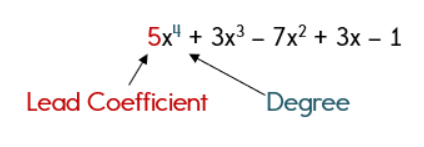
Now, for one last definition, which is actually a review! If two or more terms have exactly the same variables, then they are called like terms.
Like Terms
Okay... now you are ready to dive into the polynomials unit! If you are new to Polynomials, I would suggest starting with adding polynomials.
Good luck - you can do it!
Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.
Need Help? Try This Online Calculator!
Affiliate Products...
On this site, I recommend only one product that I use and love and that is Mathway If you make a purchase on this site, I may receive a small commission at no cost to you.
Comments
We would love to hear what you have to say about this page!