Simplifying Algebraic Expressions and Combining Like Terms

There are two things that you must be able to do when simplifying algebraic expressions. The first is to be able to use the distributive property.

The second math concept that you must understand is how to combine like terms. Before we dive into analyzing "like terms", let's first discuss what a term is and the vocabulary associated with terms.


What is a Term?

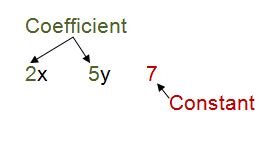
Take a look at these three terms.

2x is a term, 5y is a term, and 7 is a term.

The 7 does not have a variable. It is called a constant. Since it doesn't have a variable, its' value will always remain the same, 7. That's why it is called a constant.

The 2 in the term 2x is called a coefficient. A coefficient is a number by which a variable is multiplied. The 5 in the term 5y is also a coefficient.

So, now you know what these important vocabulary words mean: A constant is a term that is just a number, it does not contain a variable. A coefficient is the number that you multiply by a variable.

Ok.. now moving onto like terms.


What Are Like Terms?

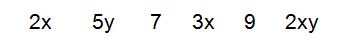
Let's take these six terms above as our examples.

Like terms are two or more terms that have EXACTLY the same variables. (The coefficients do not have to be the same, just the variables!)

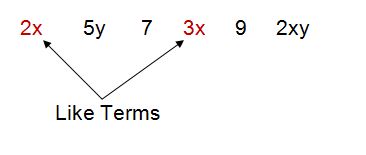
For example, for the 6 terms above, 2x and 3x are like terms because they both just contain an x.


Can you find the other set of like terms?


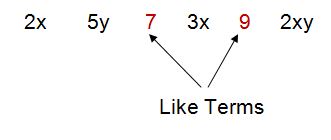
Yes, 7 and 9 are like terms. 7 and 9 are like terms because they are both constants. Neither of them have a variable and that is what makes them like terms.



What Does Not Have a Like Term?

5y does not have a like term because no other term has the variable y. 2xy does not have a like term because no other term has the variables x and y.

Ok, enough vocabulary... let's look at a few examples. We are going to simplify each expression by combining like terms.


Tip for Combining Like Terms

Each term is separated by a plus sign or a minus sign.

When you combine like terms, you MUST take the sign in front of the term with it or your answer may be incorrect!



Example 1- Combining Like Terms


I like to rewrite my like terms together. I feel that it makes it easier to compute and will help you to not lose your sign when you a lot of terms to combine.



Example 2 - Subtraction Signs Make It Tricky!


Ok, are you confident enough to use the distributive property when simplifying algebraic expressions? Sure you are, let's go!

If you see an addition or subtraction problem inside a set of parenthesis, you must use the distributive property BEFORE simplifying the expression.

As you review the next example, notice how the distributive property was used first, then the algebraic expression was simplified.


Example 3 - Using the Distributive Property


Ok... with three great examples, you should be ready to try some on your own!

You can try a few practice problems here on the Simplifying Algebraic Expressions Practice Page.



  • Simplifying Expressions

    • Comments

    We would love to hear what you have to say about this page!

    Need More Help With Your Algebra Studies?

    Get access to hundreds of video examples and practice problems with your subscription! 

    Click here for more information on our affordable subscription options.

    Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.