Graphing a Linear Equation
Using Slope Intercept Form

Now that you've completed a lesson on graphing slope you are finally ready to graph linear equations.

There are several different ways to graph linear equations. You've already learned how to graph using a table of values. That's okay for the beginner, but it can be a little time consuming.

Using slope intercept form is one of the quickest and easiest ways to graph a linear equation.

Before we begin, I need to introduce a little vocabulary. We are going to talk about x and y intercepts.

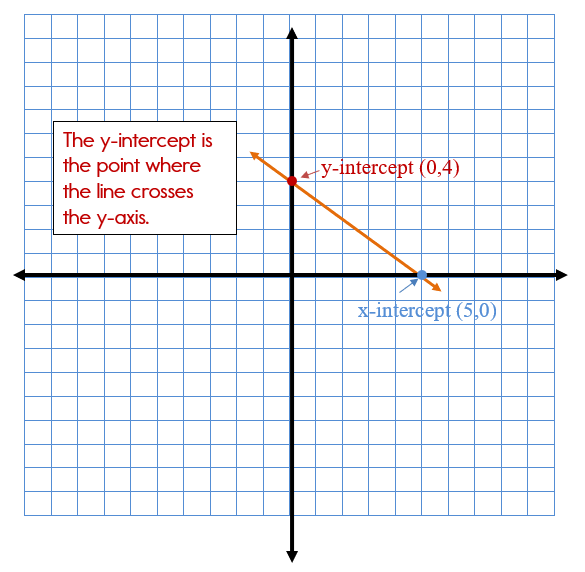
An x intercept is the point where your line crosses the x-axis. The y intercept is the point where your line crosses the y-axis.

We are only going to focus on the y intercept in this lesson, but you'll need to know x intercept for later.

Let's take a look at intercepts.

---

---

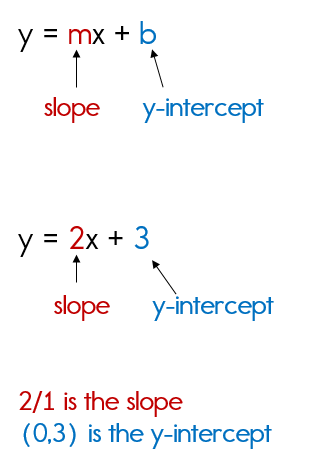
Slope intercept form is used when your linear equation is written in the form:

y = mx + b

x and y are your variables. m will be a numeral, which is your slope. b will also be a numeral and this is the y-intercept.

In this form only (when your equation is written as y = ....) the coefficient of x is the slope and the constant is the y intercept.

When an equation is written in this form, you can look at the equation and have enough information to graph the equation.

Take a look...

Slope Intercept Form

---

Let's look at a few examples and I promise that you'll LOVE this new way of graphing!

Example 1: Graphing Using Slope Intercept Form

---

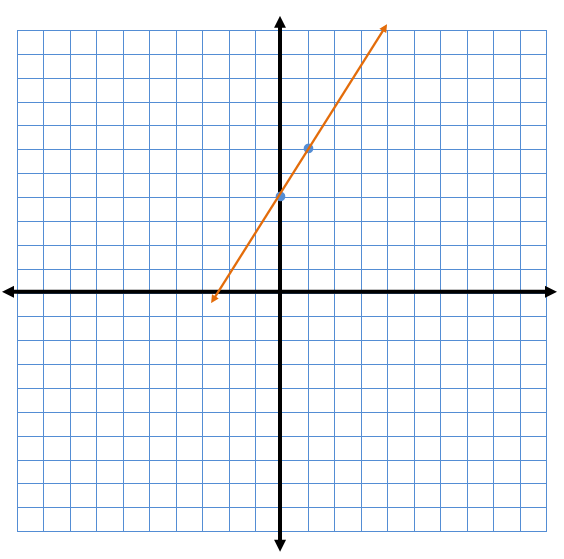
Graph the equation: y = 2x + 4

Before we begin, let's identify the slope and y-intercept.

Slope = 2  or 2/1

Y-intercept = 4  or (0,4)

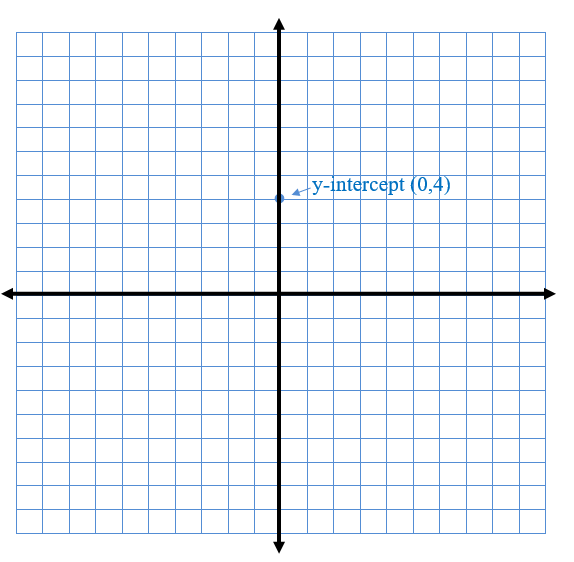
Step 1: Plot the y-intercept on your graph. The y-intercept is 4, so I will plot the point (0,4)

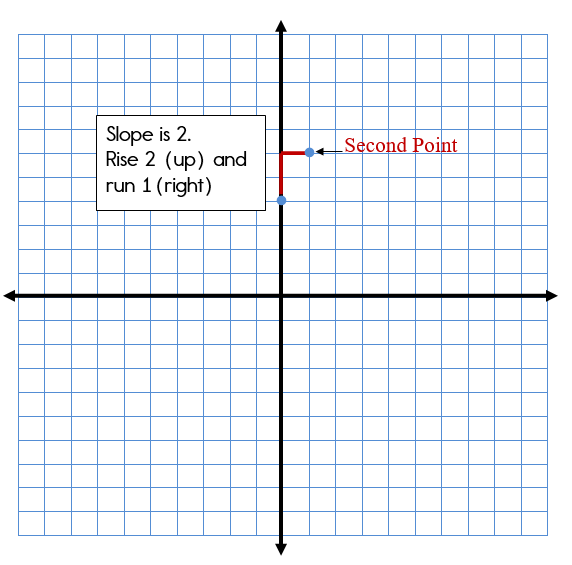
Step 2: From the y-intercept (0,4) use the slope to plot your next point.

              The slope is 2, so you will rise 2 (up) and run 1 (to the right).

Step 3: Draw a line through your two points.

This line represents the equation   y = 2x + 4.

Every point on this line is a solution to this equation.

Need a little more clarification? No problem, just check out the following video. Example 1 will be explained again step by step.

Let's take a look at one more example.

In this example, we will graph an equation that has a negative slope.

Example 2: A Negative Slope

---

Graph the equation, y = -1/3x

Let's first identify the slope and y-intercept.

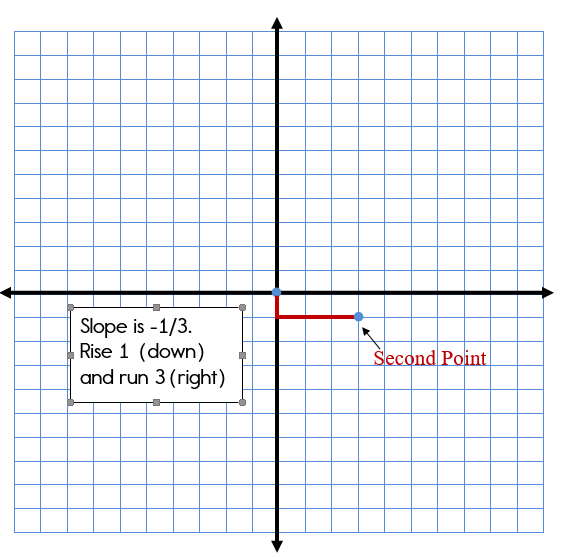
The slope is -1/3.

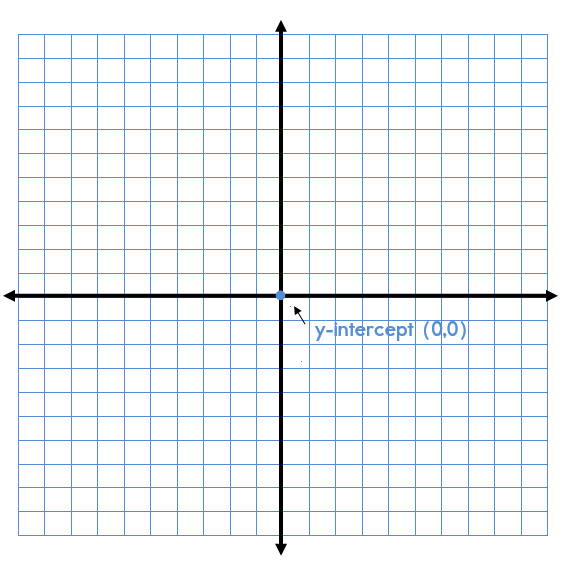
The y-intercept is 0. Since there is no number value for b, the y-intercept is 0. This means that the y-intercept is at the origin or (0,0).

Step 1: Plot your y-intercept. (0,0).

Step 2: The slope is -1/3. Therefore, from the y-intercept, we will count down 1 and right 3. Then plot your next point at (-1,3).

Step 3: Draw a line through your two points.

This line represents the equation   y = -1/3x.

Every point on this line is a solution to this equation.

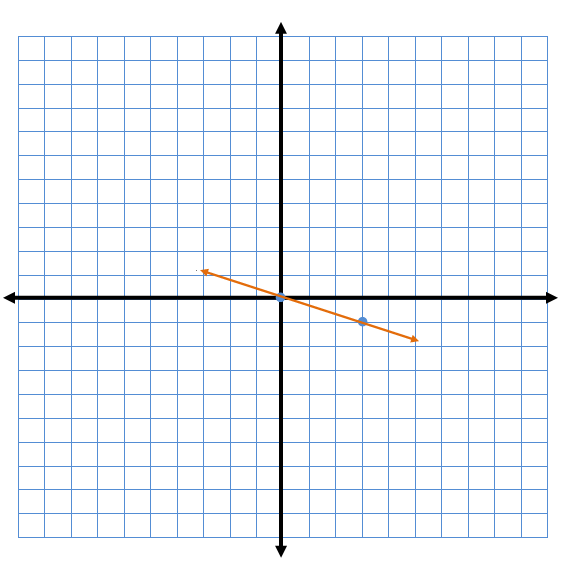
Notice that the slope in this equation is negative. This means that our line must be "falling" from left to right.

Always double check your line and your slope. If your slope is positive, then your line should "rise" from left to right. If your slope is negative, then your line should "fall" from left to right.

Here's a quick summary of this lesson:

1. Home
>
2. Graphing Equations
>
3. Slope Intercept Form

---

---

Copyright © 2009-2020   |   Karin Hutchinson   |   ALL RIGHTS RESERVED.