Basic Algebra Formulas
Here you'll find links to all algebra formulas on this page.
- Laws of Exponents
- Multiplying Polynomial Formulas
- Special Factoring Formulas
- Quadratic Equation Formulas
- Pythagorean Theorem
Laws of Exponents
There are several different "laws" or properties when working with exponents:
For detailed examples on how to use the laws of exponents, click here.
Next we'll look at a few formulas that can be used when working with polynomials.
Polynomial Formulas
There are special rules or formulas that can be used when multiplying polynomials or factoring polynomials. Let's take a look:
Multiplying Polynomials Using FOIL
To multiply two polynomials, multiply each term in the first polynomial by each term in the second polynomial. This is also known as using FOIL.
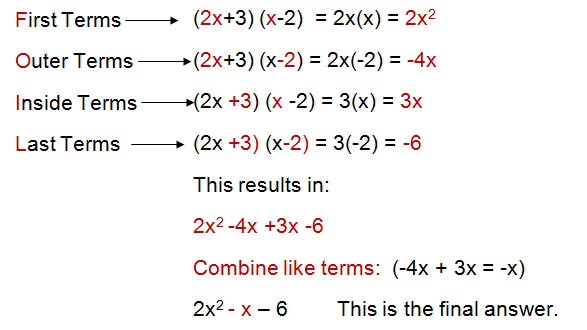
For detailed examples on using the FOIL Method, please click here.
Square of a Binomial
o square a binomial, you add: the square of the first term, twice the product of the two terms, and the square of the last term. Take a look:
Click here for step by step examples on squaring a binomial.
Difference of Two Squares
When two binomials differ only by the sign between their terms (one a plus, the other a minus), we call this a Difference of Two Squares.
The rule is very easy to remember: Subtract the square of the second term from the square of the first term. Take a look:
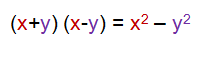
Step by step examples of problems involving a difference of two squares can be found here.
Polynomials - Special Factoring
The following formulas will actually take our special products from above and work backwards to factor. Same rules, we are just working backwards to find the factors.
Perfect Square Trinomial
A perfect square trinomial results in binomial squares.
If you notice that the first and last terms are perfect squares, then check to see if the trinomial factors as a binomial square.
Difference of Two Squares
The Sum and Difference of Two Cubes
The following are the formulas for factoring the sum and difference of two cubes:
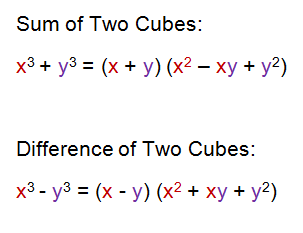
Quadratic Formula
ou can use the quadratic formula to solve ANY quadratic equation. It is used most when the quadratic equation is non-factorable.
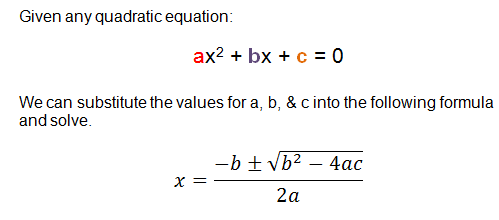
Click here to see step-by-step examples using the quadratic formula.
Vertex Formula
The vertex formula is used when you must find the vertex (minimum or maximum point) of the parabola.
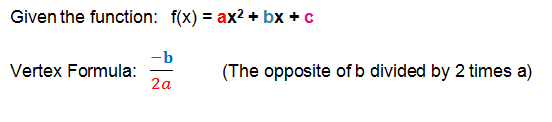
Click here for detailed examples on using the vertex formula.
Pythagorean Theorem
The Pythagorean Theorem is used to identify the length of the sides of any right triangle.
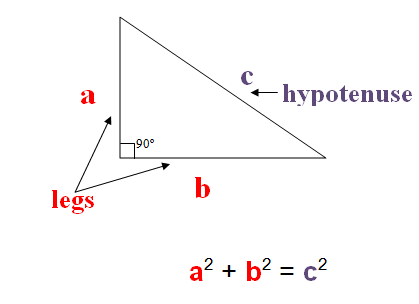
Click here for detailed examples on using the Pythagorean Theorem.
Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.
Need Help? Try This Online Calculator!
Affiliate Products...
On this site, I recommend only one product that I use and love and that is Mathway If you make a purchase on this site, I may receive a small commission at no cost to you.
Comments
We would love to hear what you have to say about this page!