Using the Vertex Formula
Quadratic Functions - Lesson 2
Before we begin this lesson on using the vertex formula, let's briefly recap what we learned in lesson 1.
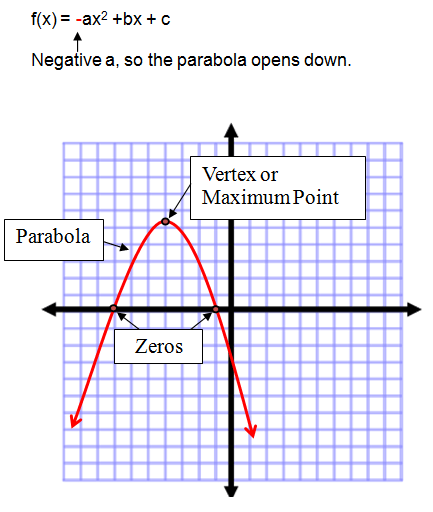
A quadratic function can be graphed using a table of values. The graph creates a parabola. The parabola contains specific points, the vertex, and up to two zeros or x-intercepts. The zeros are the points where the parabola crosses the x-axis.
If the coefficient of the squared term is positive, the parabola opens up. The vertex of this parabola is called the minimum point.
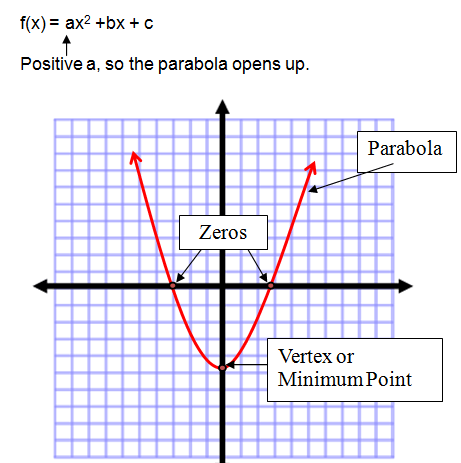
If the coefficient of the squared term is negative, the parabola opens down. The vertex of this parabola is called the maximum point.
In the previous lesson, you graphed quadratic functions using a table of values. In that lesson, I gave you the x values within the table of values.
How would you know which x values to choose if you were graphing a quadratic function on your own? How would you be sure that you chose an x value that allowed you to graph the vertex? This point is essential for graphing a parabola.
There is a special formula that you can use to find the vertex. Once you know the vertex, you can be sure that you have the essential point for graphing the parabola!
Don't forget to check out the Algebra Class E-courses if you get confused. There you will find many examples on video and a lot of practice problems.
The Vertex Formula
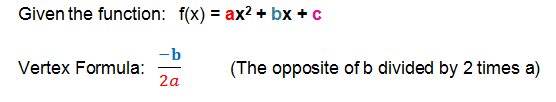
Now, let's look at an example where we use the vertex formula and a table of values to graph a function.
Example 1
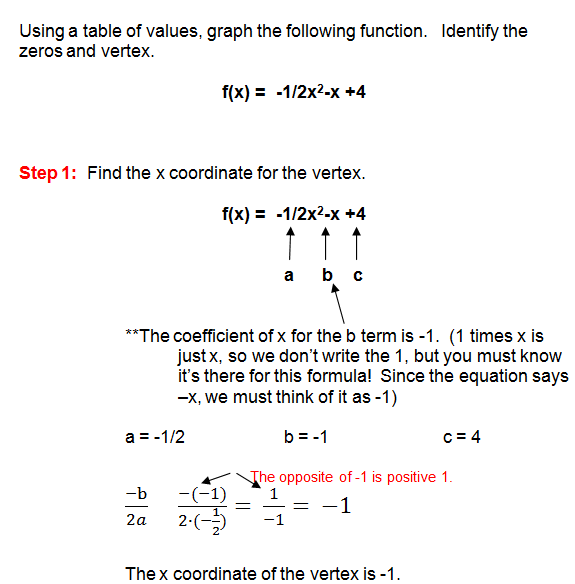
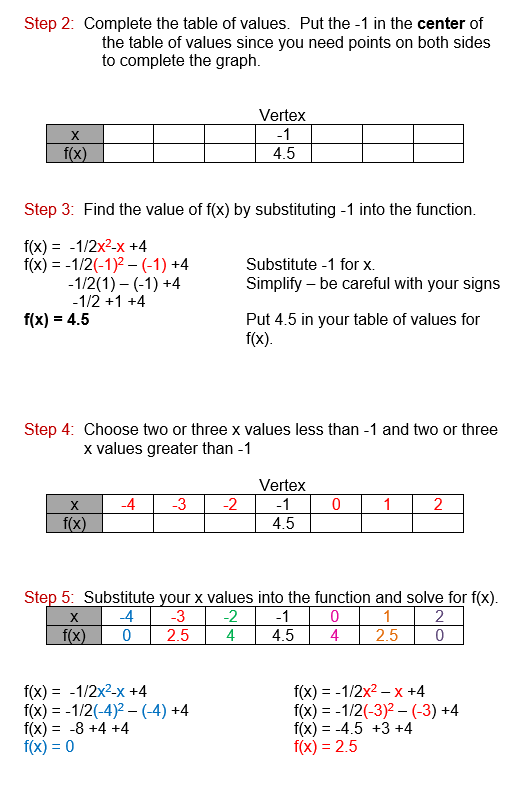
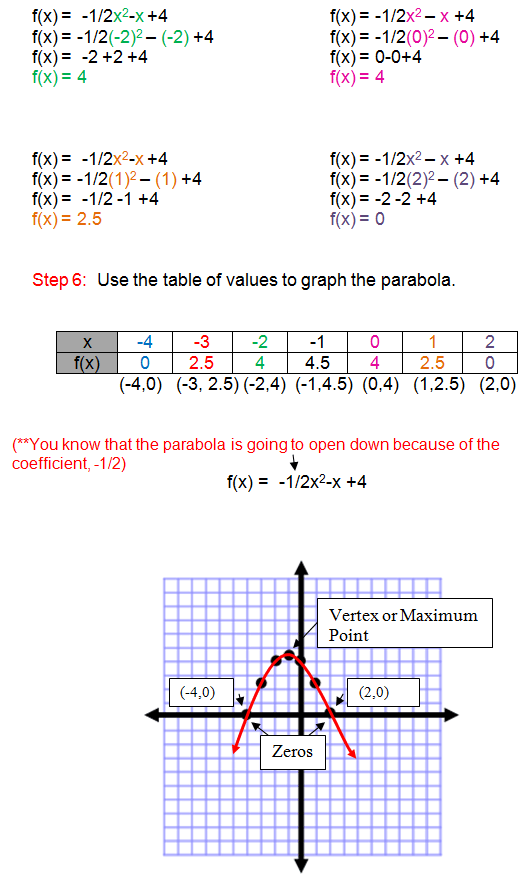
The vertex, also known as your maximum point, is (-1, 4.5). The zeros of the function are: (-4,0) and (2,0). These are the points where the parabola crosses the x-axis.
Are you having trouble finding the vertex or graphing your homework problems? Use Algebrator Software to graph ANY parabola.
Ok, ready to try one on your own?
Practice Problems
Given the following function:
f(x) = 1/2x2 - x +2
Predict whether the parabola will open up or down.
Find the x coordinate of the vertex using the vertex formula.
Create a table of values and graph the parabola.
Identify the zeros of function.
Click here to print out graph paper.
Answer Key
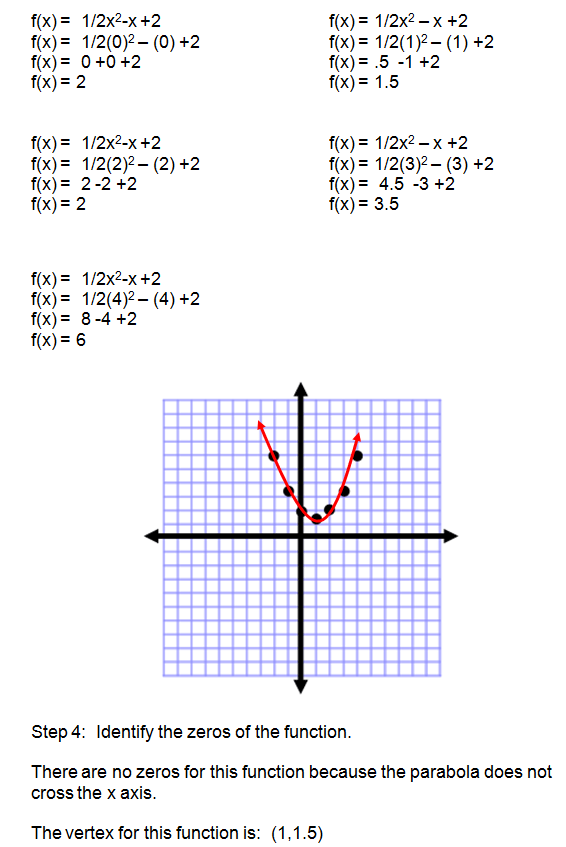
Great Job! This concludes our lesson on quadratic functions!
Now you are ready to move onto Step and Discontinuous Functions.
|
