Algebra Functions

You are now deeper in your Algebra journey and you've just been introduced to this term called a "function". What in the world is a function?

Although it may seem at first like a function is some foreign creature in Algebra land, a function is really just an equation with a fancy name and fancy notation.

If you are nervous, Algebra Class offers many lessons on understanding functions. Click here to view all function lessons.

Ok, so getting down to it, let's answer that question: "What is a function?"


A function is a relationship between two variables. The first variable determines the value of the second variable. The value of the first variable corresponds to one and only one value for the second variable.


Yes, I know that these formal definitions only make it more confusing. Let's take a look at this another way.

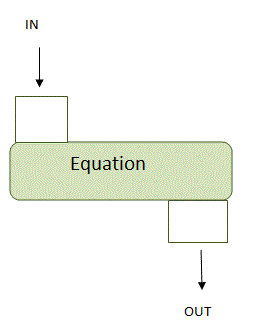
I always go back to my elementary years when we learned about functions - but never called them functions. We had what was known as an "in and out box". Some teachers now call it a "Function Box" and this is why:

Here's a picture of an algebra function box. Imagine the equation being the center of the function box. You put a number in, the function box performs the calculation and out pops the answer.

algebra function machine


Let's take a look at an example with an actual equation. Here we have the equation:
y = 2x+1 in the algebra function box. (Notice how our equation has 2 variables (x and y)

When we input 3, the function box then substitutes 3 for x and calculates the answer to be 7. (2*3 +1 = 7). This means that the variable y = 7.

algebra function example

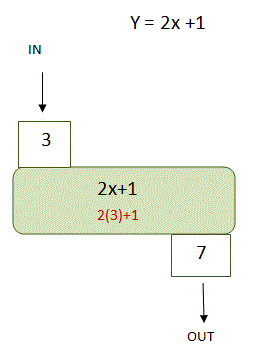
The equation y = 2x+1 is a function because every time that you substitute 3 for x, you will get an answer of 7. When x = 3, y = 7 every time. No other number will correspond with 3, when using this equation.

If you input another number such as 5, you will get a different output. When you input 5, you should get 11 because (2*5+1 = 1), so when x = 5, y = 11. No other number can correspond with 5, when substituting into this equation. Therefore, this equation can be labeled a function.


It seems pretty easy, right? It seems like all equations would be considered functions. Take a look at an example that is not considered a function.

Let's take the equation: x = y2.

When we input 4 for x, we must take the square root of both sides in order to solve for y. We end up with y = 2 or -2.

function examples

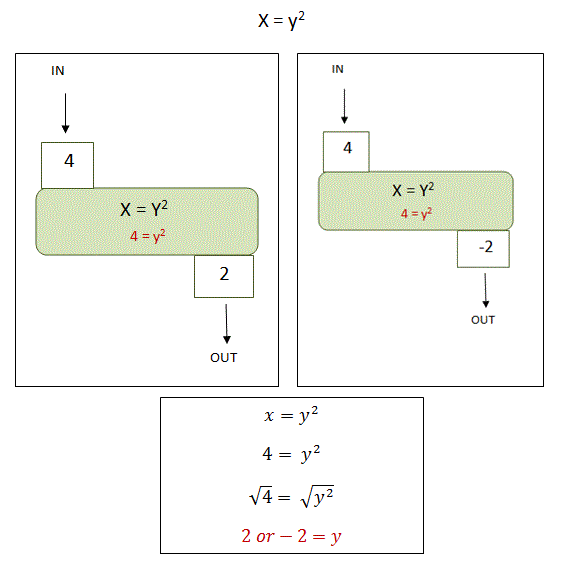
We cannot say that the equation x = y2 represents a function because when we input 4 for x, we get two different answers for y (2 and -2). Therefore, this does not satisfy the definition for a function: "the value of the first variable corresponds to one and only one value for the second value". We have more than one value for y.


Hopefully with these two examples, you now understand the difference between an equation that represents a function and an equation that does not represent a function. You will find more examples as you study the lessons in this chapter.

So, what kinds of functions will you study? In Algebra 1, we will study linear functions (much like linear equations) and quadratic functions. As you progress into Algebra 2, you will be studying exponential functions.

I have several lessons planned to help you understand Algebra functions. Take a look.


Below is the table of contents for the Functions Unit. Click on the lesson that interests you, or follow them in order for a complete study of functions in Algebra 1.

Functions Unit

  1. Algebra
    2. >
  2. Functions

Comments

We would love to hear what you have to say about this page!

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.