Using the Distributive Property
The distributive property is used A LOT in Algebra! It is essential that you MASTER this skill in order to solve algebraic equations.
First we are going to make sure that you have the proper background knowledge, so let's look at a simple math problem:
2(3 + 4) = ?
2(7) = 14
Since this problem contains all numerals, we can use the order of operations and solve inside the parenthesis first.
We know that 3 + 4 = 7 and then multiply 7 by 2 and we get our answer of 14! That's basic math.
But, in Algebra we often don't know one of the numeric values and a
variable (letter) is used in it's place. Let's look at another example:
2(x + 4) = ?
In this problem, we don't know the value of x, so we can't add x + 4. But... we do want to simplify it a little further by removing the parenthesis. So, this is when the distributive property comes in handy.
To prove that this property works, look at the model below.
A Visual Representation of the Distributive Property
This is a model of what the algebraic expression 2(x+4) looks like using Algebra tiles.
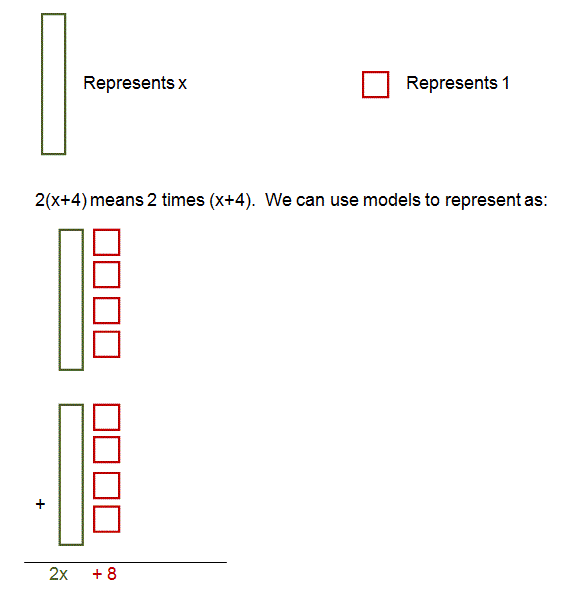
The problem 2(x+4) means that you multiply the quantity (x +4) by 2. You could also say that you add (x+4), 2 times which is the way it is shown in the model. You can see we got an answer of 2x + 8 using the models.
We would get the same answer using the distributive property! Let's take a look.

Here's a couple of other examples for you to study. Copy the examples onto your paper and do them with me.
Example 1 - The Distributive Property

Example 2 is very similar to example 1 above. The only difference is the minus sign. Inside of the parenthesis, we have the expression (x-7), so notice how my answer also contains the minus sign.
Example 2 - Distributive Property with a Minus Sign

In example 3, I'd just like to point out that sometimes you may have a coefficient with x. For example, inside of the parenthesis, we have the expression (4x - 5). You can still multiply 2 times 4x to get 8x.
Example 3 - More Distributing

For example 4, notice that we are distributing a negative number. This becomes tricky because we have to pay careful attention to our signs. Take a look.
Example 4 - Distributing a Negative Number

TIP: When you simplify algebraic expressions, you DO NOT want two math symbols following each other!
For example: -3x + (-4) is incorrect. See how the plus sign is followed by the negative sign? This is better read as -3x - 4.
-3x - (-4) is incorrect. See how the minus sign is followed by the negative sign? This is better read as -3x + 4.
If you have two math symbols following each other, change the math sign to it's opposite (plus to minus or minus to plus)and change the negative sign following to a positive!
- Subtracting a negative is the same as adding a positive.
- Adding a negative is the same as subtracting a positive.
The distributive property is also used when solving equations. Click here if you are solving equations and need to know how to use the distributive property.
Ready to Try a Few On Your Own?
Click here to try a few practice problems.

Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.





Comments
We would love to hear what you have to say about this page!