Solving Compound Inequalities
n our last lesson, you were introduced to compound inequalities. In this lesson, we are going to take the next step and begin solving compound inequalities.
Hopefully you have studied our lesson on solving regular inequalities. If so, I think you'll find this lesson to be pretty easy. The only tricky part at times is graphing the solutions. Let's take a look at a couple of examples together.
In this lesson, we are only going to focus on conjunction compound inequalities. In our next lesson, we will focus on disjunction compound inequalities.
Example 1: Compound Inequalities
Solve and graph the following inequality: 10 < 2x + 8 < 16
Notice that this is a "conjunction" inequality. Conjunction inequalities usually include the word "and".
If we were to read this aloud, we would say, "10 is less than 2x + 8 AND 2x+8 is less than 16". Notice how the word "and" separates this into two inequalities?
There are actually two different ways to solve this inequality. This first method is to separate this into two different inequalities and solve each independently. The second method is to solve both parts at the same time. I will show you both ways and you can decide which is best for you.
Method 1: Solve Two Inequalities Independently
For this method, we will use the word "and" to write two different inequalities.
Take note of how the expression in the middle is used twice in order to write two different inequalities.
10 < 2x + 8 < 16
|
10 < 2x + 8 10 - 8 < 2x + 8 - 8 2 < 2x 2/2 < 2x/2 1 < x OR x > 1 |
2x + 8 < 16 2x + 8 - 8 < 16 - 8 2x < 8 2x/2 < 8/2 x < 4 |
Notice how we solved each equation independently.
Now let's graph the equation on a number line.
Graph each equation separately and then find the intersection. This is your final solution.
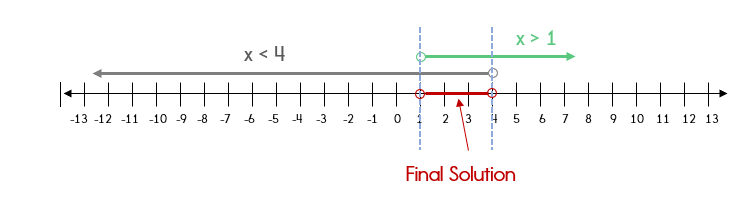
What does this final solution mean?
This means that only the numbers greater than 1 and less than 4 will be true statements when substituted into this compound inequality.
Let's prove it. We will substitute 3 which is included in the solution set and then we will substitute 5 which is not included.
|
Substitute 3 10 < 2x + 8 < 16 10 < 2(3) + 8 < 16 10 < 6 + 8 < 16 10 < 14 < 16 Is this a true statement? Yes, 10 is less than 14 and 14 is less than 16. |
Substitute 5 10 < 2x + 8 < 16 10 < 2(5) + 8 < 16 10 < 10 + 8 < 16 10 < 18 < 16 Is this a true statement? No, 10 is less than 18 BUT 18 is NOT less than 16. Therefore, 5 is not a solution and that is why it's not included in the solution set. |
You may be thinking, "Wow, that seems like a lot of work for one problem." I have to agree with you. This first method does require more work since you have to solve two different inequalities.
Method 2, which I will show you next, is going to require less work because you can solve both parts of the equation at the same time. This is the method that I prefer.
Method 2: Solving Both Parts at the Same Time
We are going to solve this same inequality a different way. Instead of separating this into two inequalities, we are going to leave it as one."
Remember my famous saying for solving equations, "Whatever you do to one side of the equation, you must do to the other side?"
Well, we are going to change that saying just a little to, "Whatever you do to one side of the equation, you must do to ALL sides of the equation."
Notice that I just changed the word "other" side to "all" sides. Why? Because we are going to think of this inequality as having THREE sides. Take a look...
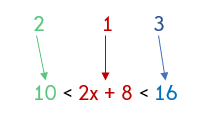
Part 1 is the part of the inequality that needs to be solved for x.
Parts 2 and 3 are the answers. So, it's like having two different answers to the same inequality.
So, whatever you do side 1, you must also do to sides 2 and 3. This of it this way and you'll have no problems. Ready to solve?
10 < 2x + 8 < 16
10 - 8 < 2x + 8 - 8 < 16 - 8 Subtract 8
2 < 2x < 8 Simplify
2/2 < 2x/2 < 8/2 Divide by 2
1 < x < 4 Final Answer
Notice how we arrived at the same answer?
Now let's graph. This solution means that solutions for x are between 1 and 4. 1 and 4 are open circles due to the less than symbols.
Remember, these two examples are two different ways to solve the same problem. You get to choose which way works best for you!
We are going to look at one more problem together. Have you been wondering about the rule that states, "If you multiply or divide by a negative number then you should reverse your inequality sign"?
Well, that rules still applies. Take a look with me...
Example 2: Compound Inequalities
-12 < -4x + 4 < 16 Original Problem
-12 - 4 < -4x + 4 - 4 < 16 - 4 Subtract 4
-16 < -4x < 12 Simplify
-16/-4 < -4x/-4 < 12/-4 Divide by -4
4 > x > -3 Divide by a negative - Reverse the signs!
This answer is now sort of written backwards. It would be much easier to graph if we reversed the sides with the smaller number first.
If we reverse sides, we must also reverse the signs.
This can also be written as:
-3 < x < 4
This means that our graph should show the solutions for x between -3 and 4, but not including -3 and 4 (open circles).
Hopefully you have a better understanding of solving conjunction compound inequalities. Just remember to follow the same rules as for regular inequalities, but now you are solving two inequalities within one problem.
In the next lesson, you will solve disjunction compound inequalities. These are the inequalities with the word "or".
Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.
Need Help? Try This Online Calculator!
Affiliate Products...
On this site, I recommend only one product that I use and love and that is Mathway If you make a purchase on this site, I may receive a small commission at no cost to you.
Comments
We would love to hear what you have to say about this page!