Subtracting Fractions with Unlike Denominators

Are you trying to plow through that fractions unit, but feeling frustrated because you still can't figure out the concept of subtracting fractions with unlike denominators?

If so, you are not alone. My statistics show that more people seek help with fractions than any other math concept.

The good news is, you can wave goodbye to your frustrations!

I am going to walk you step-by-step through several examples and by the end you will feel confident with subtracting fractions with different denominators. I promise!

Let's take a look at Example 1.


Example 1 - Subtracting Fractions with Unlike Denominators


Not too bad, right? In that example one of the fractions happened to have a denominator that was the least common denominator.

Notice how once the denominators are the same, all we need to do is subtract the numerators.

Steps for Subtracting Fractions with Unlike Denominators

1. Identify the least common denominator by finding the least common multiple for the denominators.

2. Write equivalent fractions (making sure that each equivalent fraction contains the least common denominator (LCM))

3. Subtract the numerators of the equivalent fractions that you wrote in step 2. (The denominators should now be the same.)

4. Simplify if necessary.


Jot those 4 steps down if you are having trouble remembering the steps for subtracting fractions.

Let's take a look at another example. This time, neither denominator is the least common denominator. I will also demonstrate how to subtract fractions that are written vertically.


Example 2 - Subtracting Fractions Vertically


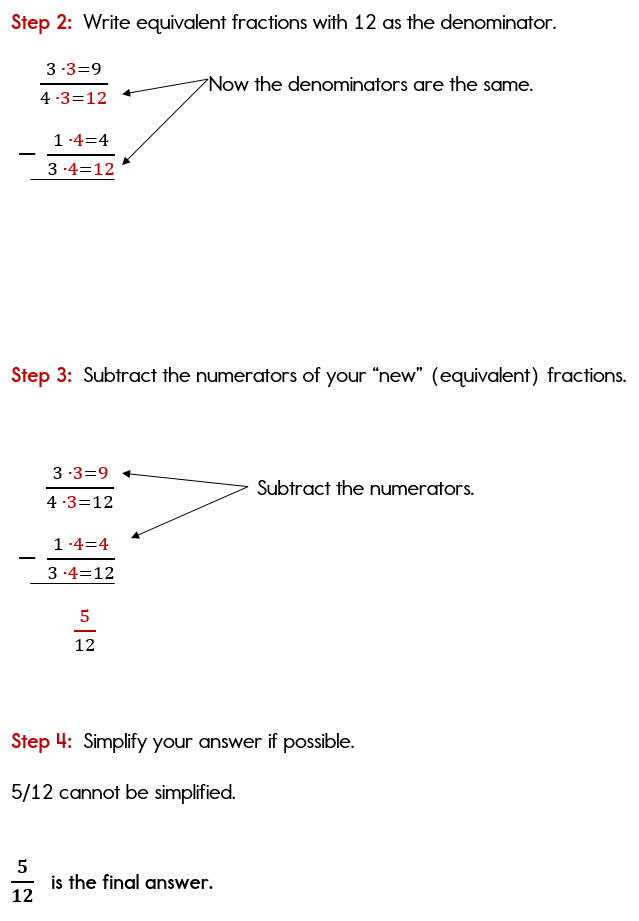
Will you work with integers (positive and negative numbers) when working with fractions?

Yes, absolutely! Let's take a look!


Example 3 - Can you have a negative fraction?


So, do you feel more confident with subtracting fractions with different denominators? I hope so! You may be ready to start adding or subtracting mixed numbers.



  1. Home
    2. >
  2. Fractions
    3. >
  3. Subtracting Fractions



Comments

We would love to hear what you have to say about this page!

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.