Solving Systems of Equations
Using Linear Combinations (Addition Method)

There are two ways to solve systems of equations without graphing. You can use the substitution method or linear combinations (which is also commonly known as the addition method).

This lesson is going to focus on using linear combinations, which is typically used when both equations are written in standard form.

The following steps are a guide for using Linear Combinations. Don't worry, it will make a lot more sense as we look at a few examples.




Steps for Using Linear Combinations (Addition Method)

  • Arrange the equations with like terms in columns.

  • Analyze the coefficients of x or y. Multiply one or both equations by an appropriate number to obtain new coefficients that are opposites

  • Add the equations and solve for the remaining variable.

  • Substitute the value into either equation and solve.

  • Check the solution.

Ok... let's make these examples make sense by looking at some examples.

Our first example is the easiest example as it is already set up perfectly to use the linear combination method.

Notice how the 3y and -3y will cancel out and leave only the x variables.


Example 1: Given Problem Has Opposite Terms

Solve the following system of equations using linear combinations (or the addition method).

4x + 3y = 5

2x - 3y = 7


Solution

Solving a system using linear combinations


The next problem isn't set up so perfectly. It demonstrates the extra step that you need to take if your original problem doesn't have opposite terms.

If you are not given opposite terms, then you must create opposite terms.  Take a look...


Example 2: Creating Opposite Terms

Solve the following system of equations:

3x + 2y = 10

2x + 5y = 3


Solution

Using Linear Combinations to solve systems of equations

Now, let's see what happens if our system of equations happens to be the same line and we have an infinite number of solutions.


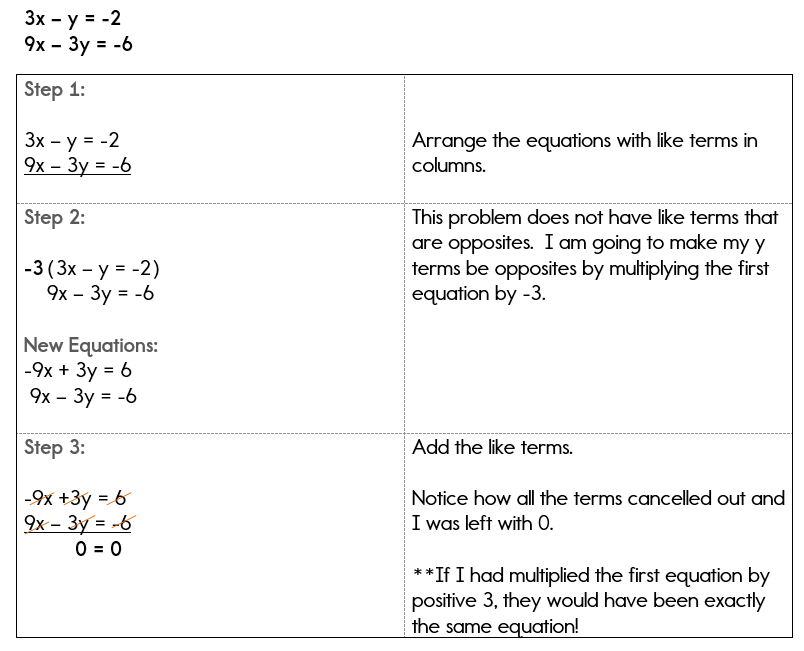
Example 3: An Infinite Number of Solutions

Solve the system of equations:

3x - y = -2

9x - 3y = -6


Solution

System of combinations solved algebraically that has infinite solutions

Notice that we end up with an expression that makes sense.  0 = 0 makes sense and this means that there are an infinite number of solution to this system of equations.  Remember, this type of graph will have two lines graphed on top of each other as they are the exact same equation.



Last example! We are going to see what happens when you try to solve a system using linear combinations that has no solution. Remember this type of problem would graph two parallel lines on a graph.

These two equations also have the same slope; however, you can't tell by looking at the equations initially because they are written in standard form.


Example 4: No Solution

Solve the following system of equations.

2x - y = 3

2x - y = -8


Solution

No solution when solving a system of equations using linear combinations

So, here again, I have a problem! 0 = -11 is NOT a true statement. Therefore, this system does NOT have a solution!

If there is no solution, then the lines are parallel. They will never intersect.


With these 4 examples, I hope that you have a better understanding of how to solve a system of equations using linear combinations.


  1. Home
    2. >
  2. System of Equations
    3. >
  3. Linear Combinations



Comments

We would love to hear what you have to say about this page!

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.