Is the Relation a Function?
Using the Vertical Line Test
A function is a relation (a set of ordered pairs) where the value of one variable depends on the value of the other variable. However, in a function, each input (x coordinate) may be paired with only ONE output (y coordinate).
Let's look at a couple of examples to clarify this definition.
Example 1
Let's look at our relation, b that we used in our relations example in the previous lesson.. Is this relation a function? Is each input only paired with only one output?
There are actually two ways to determine if a relation is a function. One way is to analyze the ordered pairs, and the other way is to use the vertical line test. Let's analyze our ordered pairs first.
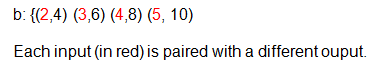
Since each input has a different output, this can be classified as a function.
Let's verify it with the vertical line test. This special test is used when you graph the ordered pairs. You imagine a vertical line being drawn through the graph. If the vertical line only touches the graph at one point, then it is a function. If the vertical line touches in more than one point, then it is NOT a function.
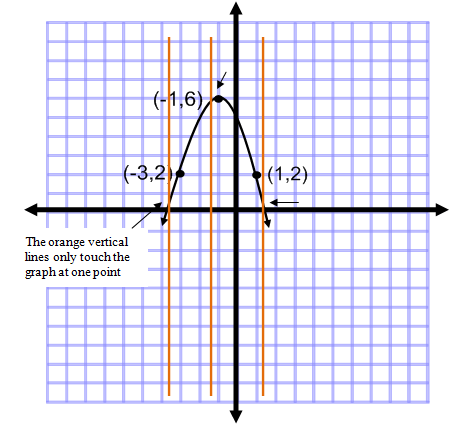
Let's graph our points and use the vertical line test to prove that this is a function. I drew the vertical lines (output) on the graph to demonstrate what it would look like. Unless asked, you really don't need to draw the vertical lines, you can just imagine the vertical line, or I have my students use the edge of a sheet of paper and move it across the graph.
Since each vertical line only touches the graph at one point, this relation can be classified as a function.
Example 2
Let's look at another example.
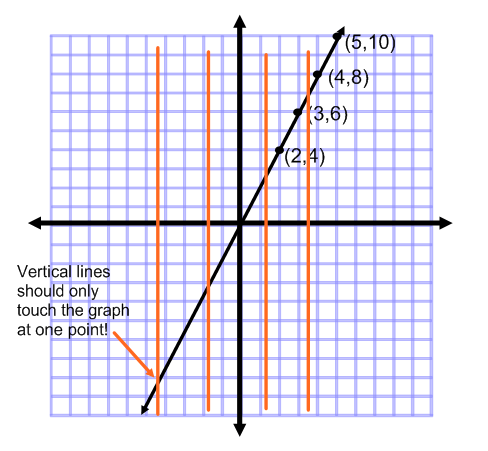
Is the relation s, a function?
s:{(-3, 2) (-1, 6) (1,2)
Let's ask ourselves: Is each input paired with only one output? (This one is a little tricky!)
YES, each input is paired with only one output. I know that you see an output of 2 twice, but each is paired with a different input. The outputs can be the same, as long as the inputs are different. Let's look at the vertical line test.
Yes, this is a function - remember that the outputs can be duplicated as long as the inputs are different.
Example 3
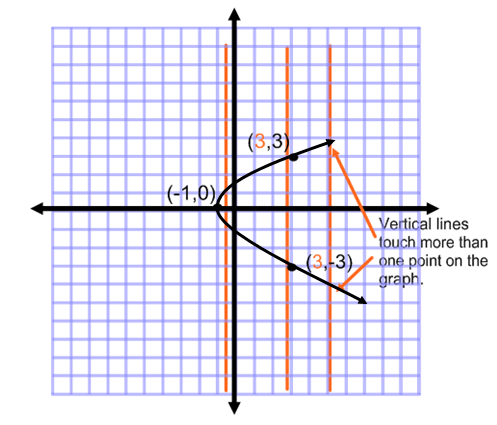
Is the relation, c, a function?
Let's ask ourselves: Is each input paired with only one output?
c:{(3,3) (-1,0) (3,-3)
NO, look at the ordered pairs - there are 2 ordered pairs with input of 3 and they have different ranges! Think about our little function machine - you cannot put in a 3 and get out a 0, and then put in another 3 and get out a -3. Each time you put in a 3, you should get the same answer.
Therefore, this relation is NOT a function. Let's look at the vertical line test.
So, how do you feel about identifying whether or not a relation is a function? I know it can be a little confusing.
Just remember: If you have duplicate inputs and they are paired with different outputs, then the relation is not a function. The vertical line test is always a good technique to use if you are unsure or want to justify your answer.
If you need more direct instruction, check out the Algebra Class E-course for video tutorials and more practice problems.
You can also try a few more practice problems right here on Algebra Class! Click here to go on to the practice.
Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.
Need Help? Try This Online Calculator!
Affiliate Products...
On this site, I recommend only one product that I use and love and that is Mathway If you make a purchase on this site, I may receive a small commission at no cost to you.
Comments
We would love to hear what you have to say about this page!