Graphing Systems of Equations

This is the first of four lessons in the System of Equations unit. We are going to graph a system of equations in order to find the solution.

REMEMBER: A solution to a system of equations is the point where the lines intersect!

Prerequisites for completing this unit: Graphing using slope intercept form .


We will begin graphing systems of equations by looking at an example with both equations written in slope intercept form. This is the easiest type of problem!


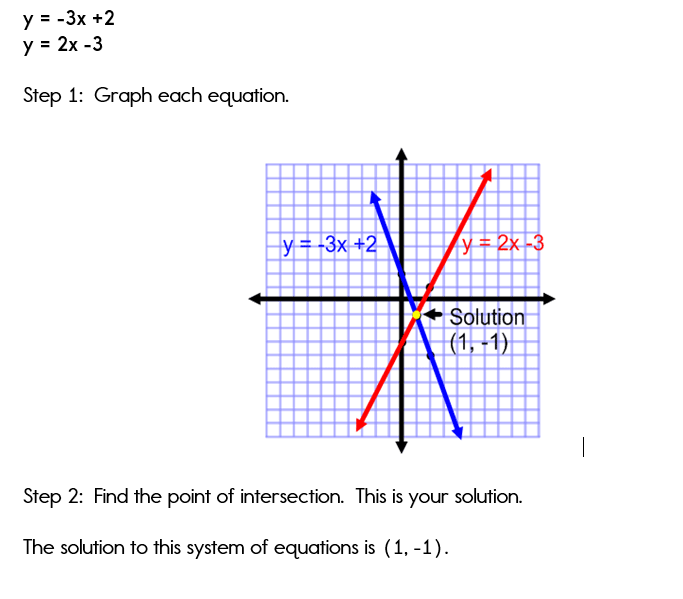
Example 1: Graphing Systems of Equations

Graph the following system of equations and find the solution.

y = -3x + 2

y = 2x - 3


Solution


Now we are going to look at a system of equations where only one of the equations is written in slope intercept form. The other equation is written in standard form.

So... what do you think we need to do first?


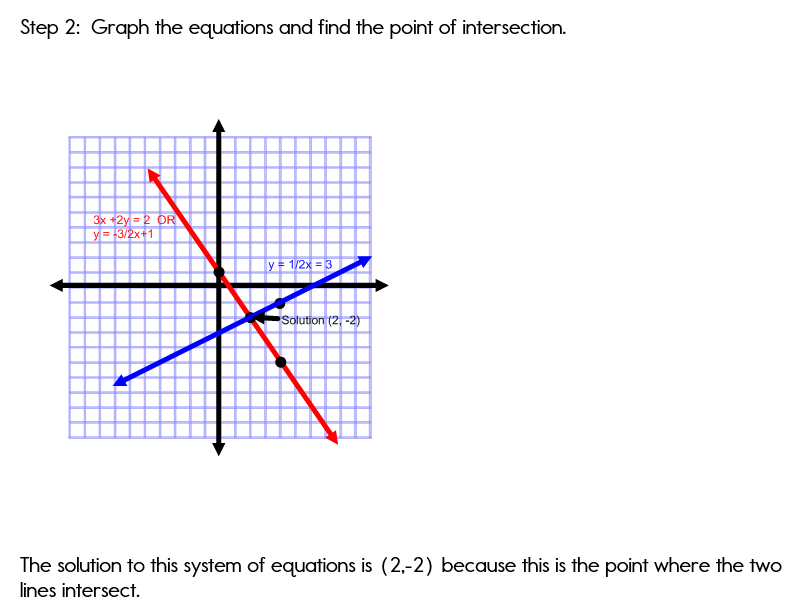
Example 2: What Happens When an Equation is Not Written in Slope Intercept Form?

Graph the system of equations and find the solution.

y = 1/2x - 3

3x + 2y = 2


Solution

Rewrite standard form equations in slope intercept form
Graphing system of equations


Now we will look at an example where there is no solution to the system of equations. Take note of what the graph looks like and why there might not be a solution.


Example 3: No Solution

Find the solution to the system of equations by graphing.

y = -1/2x + 4

y = -1/2x - 6

Solution




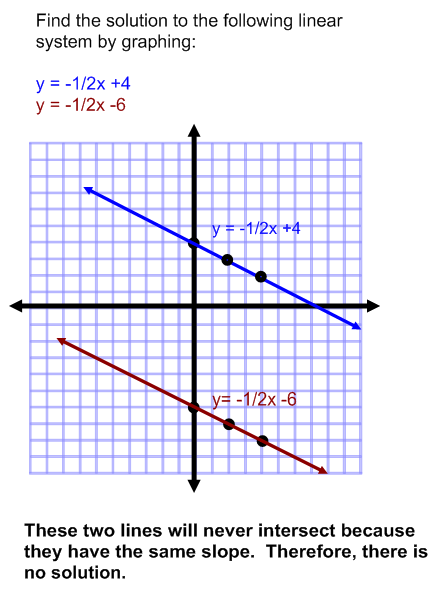
Tip

Whenever two equations have the same slope they will be parallel lines.

Parallel lines NEVER intersect. Therefore, the system of equations will NOT have a solution!


Our last example demonstrates two different things. The first is that there is more than one way to graph a system of equations that is written in standard form.

The second is that sometimes a system of equations is actually the same line, graphed on top of each other.

In this case, you will see an infinite number of solutions. It may be helpful for you to review the lesson on using x and y intercepts for this example.


Example 4: Infinite Solutions

Graph the following system of equations and identify the solution.

2x - y = 8

6x - 3y = 24


There are two ways to graph a standard form equation:

  1. Rewrite the equation in slope intercept form.
  2. Find the x and y intercepts.

When you are graphing a system of equations that are written in standard form, you can use either method.

For this particular example, we will find the x and y intercepts.


Solution

Finding the x and y intercepts
System of Equations graph with an infinite number of solutions


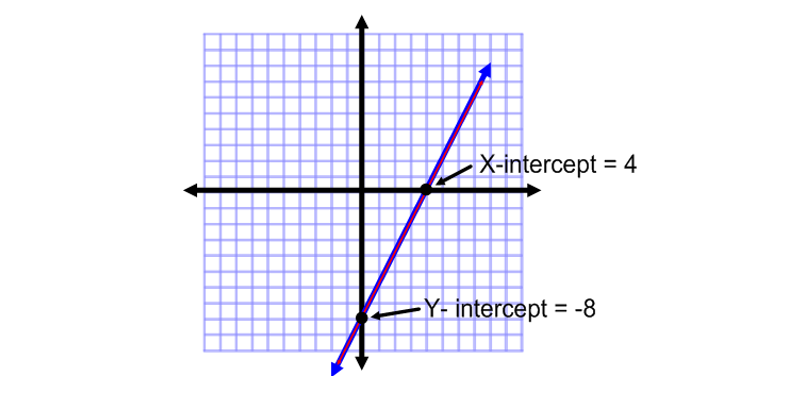
Did you notice that both equations had the same x and y intercept?

This is because these two equations represent the same line. Therefore, one is graphed on top of the other.

In this case, the system of equations has an infinite number of solutions! Every point on the line is a solution to both equations.

You've now seen all different strategies for graphing a system of equations and you've experienced what a graph looks like when there is no solution and when there are an infinite number of solutions!


If you'd like to practice a few systems of equations problems on your own, visit our Graphing Systems of Equations Practice Page.


In the next lesson, you will learn another way of solving a system of equations. You will solve a system using substitution.


  1. Home
    2. >
  2. System of Equations
    3. >
  3. Graphing Systems



Comments

We would love to hear what you have to say about this page!

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.