Using the X and Y Intercept to Graph Linear Equations

You've learned one way to graph a standard form equation - by converting it to slope intercept form. Click here to review this lesson.

There is another way to graph standard form equations, and that is to find the x and y intercepts.

Now let's review what the term intercepts means. An intercept is where your line crosses an axis. We have an x intercept and a y intercept.

The point where the line touches the x axis is called the x intercept. The point where the line touches the y axis is called the y intercept.

Take a look at the graph below.

Definition of Intercepts

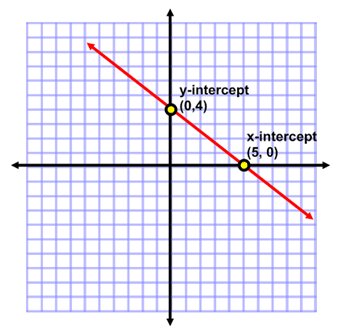
If we can find the points where the line crosses the x and y axis, then we would have two points and we'd be able to draw a line.

When equations are written in standard form, it is pretty easy to find the intercepts. Take a look at this diagram, as it will help you to understand the process.


Now, let's apply this. Just remember:


To find the X Intercept: Let y = 0


To find the Y Intercept: Let x = 0


Example 1: Graphing a Standard Form Equation

Graphing Standard Form Equations Using Intercepts


This concept can be confusing, so let's take a look at the video to explain the first example.



Ok.. now let's look at a real world problem that we can solve using intercepts.


Example 2: Solving Real World Problems

Emily received a gift card for her birthday and decided to download a few books. She downloaded a few $6 books and a few $3 books. She spent $30 on books. The equation that represents x number of $6 books and y number of $3 books is:

6x + 3y = 30

  • Graph the equation.
  • Find the x-intercept. Explain what the x-intercept means in the context of this problem.
  • Suppose Emily downloaded 3 $6 books. How many $3 books did she download?

Solution

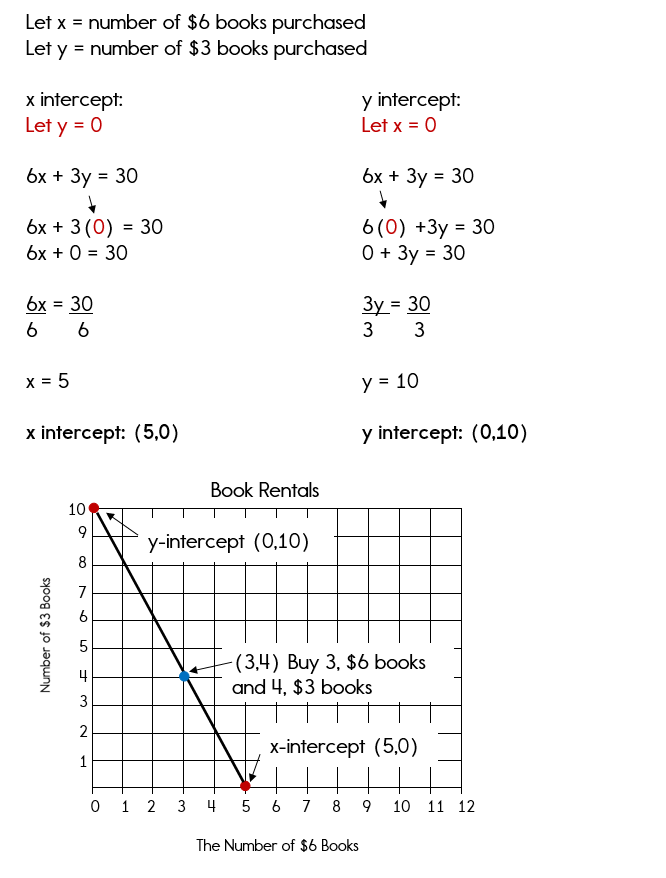
The x-intercept is (5,0). The x-intercept means that if no $3 books are purchased, Emily could purchase 5, $6 books for $30.

By reading our graph, we see that if Emily bought 3, $6 books, she could buy 4, $3 books.

Let's prove it!

6x + 3y = 30

6(3) + 3(4) = 30

18 + 12 = 30

30 = 30


It works!  Therefore, (4,3) is a solution to this problem.

Great job on graphing equations.


  1. Home
    2. >
  2. Graphing Equations
    3. >
  3. X and Y Intercepts



Comments

We would love to hear what you have to say about this page!

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.