Are You Ready to Learn How to Solve Inequalities?

Now that you've learned several methods for solving one-step equations, are you wondering how to solve inequalities? Luckily, most of the steps used to solve equations, are also used to solve inequalities.

In this lesson, we will focus on solving one-step addition and subtraction inequalities.

As you begin learning how to solve one-step inequalities, you may also be asked to graph your answer. If the inequality that you are solving contains one variable, then you will represent your answer on a number line.

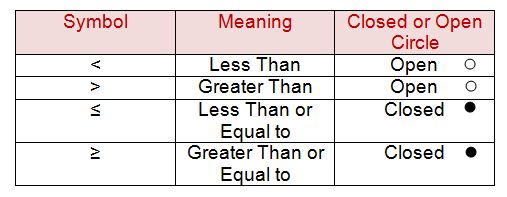
You will begin by representing your answer on the number line with a closed circle or an open circle. Take a look.....

inequality symbols

If the circle is open, then that means that the answer is less than or greater than this number, BUT NOT equal. Only if the circle is closed, can the answer be equal to this answer.

Take a look at the following examples on graphing inequalities.

Example 1

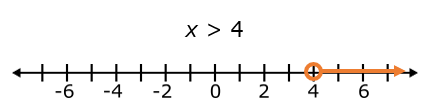
The expression says that x is greater than 4. This means that the solution set contains all numbers greater than 4.

Since the solution is greater than 4 and not equal to 4, we must use an open circle to indicate that 4 is not included.

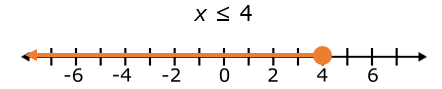
The expression says that x is less than or equal to 4. This means that the solution set contains 4 and all numbers less than 4.

Since the solution contains 4, we must use a closed circle to indicate that 4 is part of the solution set.

Now we will take a look at a few examples of how you can solve inequalities. We will also graph the solution on a number line.

Take a look at our first example. Notice how the same steps that are used to solve equations, are also used to solve inequalities.

Example 2

This answer shows that the solution set contains 10 and al numbers less than 10.



Now we'll take a look at one more example that contains a negative integer. Again, we use the exact same process that we use when solving equations

Example 3

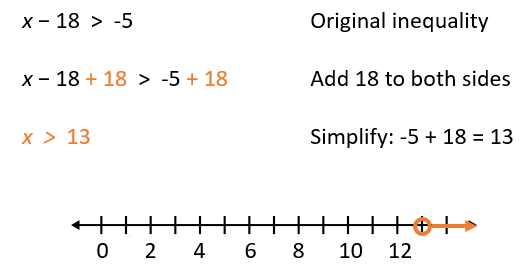
This answer shows that the solution set contains all numbers greater than 13.


Not too bad, right? When learning how to solve inequalities that deal with addition and subtraction, follow the same process as with equations. The only difference is knowing how to represent your final answer on a number line.

In our next lesson, we will continue working with one-step inequalities, but this time we will look at special rules when multiplying or dividing within inequalities.

Comments

We would love to hear what you have to say about this page!

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.