Simple Steps for Adding
Square Roots
On this page you'll find...
You'll be happy to hear that adding square roots follows many of the rules as other algebraic terms.
In fact, the most important rule is...
When Adding Square Roots You Can Only Combine "Like Terms"
Remember "like terms"? Yes, we can only add or subtract square roots (or any radical) if they are like terms.
So, let's look at a few examples.
What are Square Roots that are Like Terms?
When working with square roots, like terms will have the exact same radicand.
(Remember the radicand is the expression inside the radical)

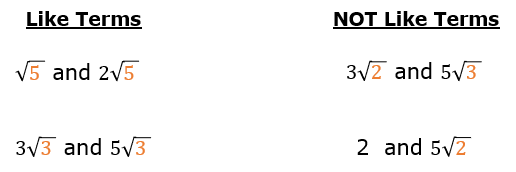
So, if your square roots are like terms, then you can add them together! Let's take a look at a few examples.
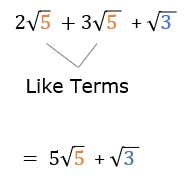
Example 1: Adding Square Roots
Notice how in this example, we can add the two square roots that have a radicand of 5. The square root of three is not a like term, so it can not be combined.
Example 2: Simplify Before Adding Square Roots
Before adding square roots, always check to see if any can be simplified. Sometimes the square roots can even be simplified to whole numbers!
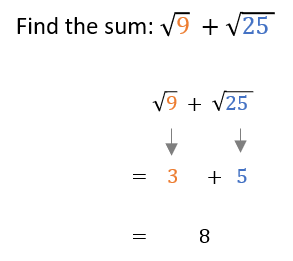
Since the square root of 9 equals 3 and the square root of 25 equals 5, this problem can be simplified to a whole number.
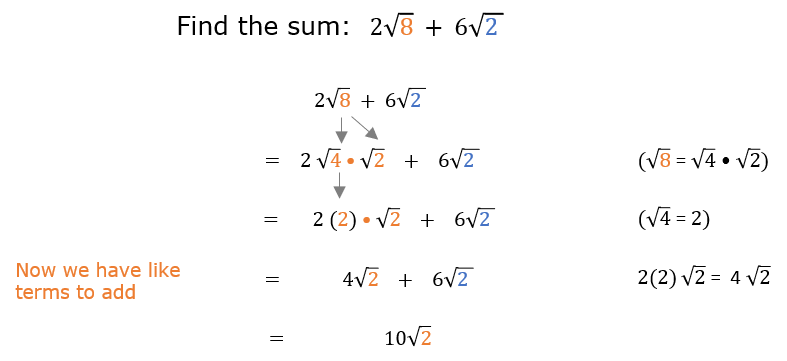
Example 3: More Simplifying Before Adding
Be careful not to automatically just assume that since your radicands are not exactly the same that you don't have like terms.
Remember that you must simplify first, then determine if you have like terms.
Notice in this next example that 2 times the square root of 8 can be simplified to 4 square roots of 2 and then this creates like terms that can be added together.
The most important thing to remember when adding square roots is that you can only add like terms.
It's also important to remember that you must always simplify square roots first and then determine if you have like terms.
I hope that these examples help you as you learn how to add square roots.

Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.

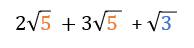
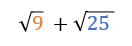
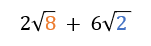





Comments
We would love to hear what you have to say about this page!