Your Step-by-Step Guide to Learning How to Simplify a Square Root
Do you feel confused when asked to simplify a square root that is not a perfect square? It can be tricky, but I'm going to break it down for you and you will be simplifying these babies in no time!
What You'll Find on This Page:
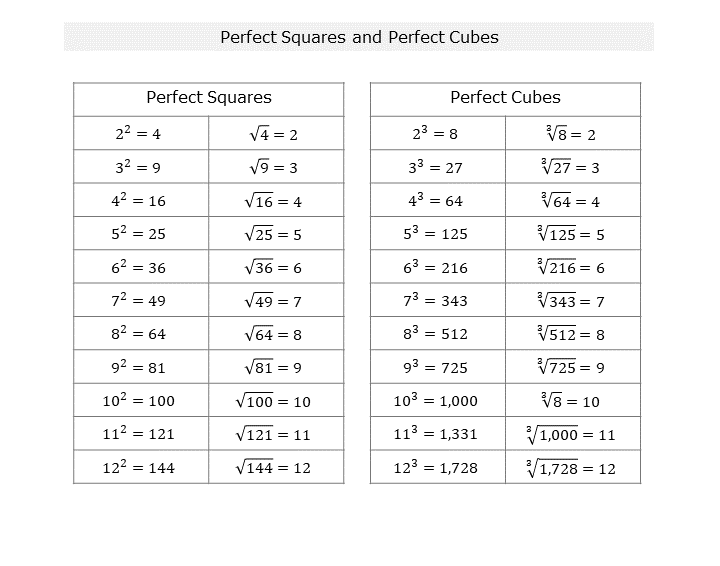
A downloadable and printable table of perfect square roots and cubes! This is a great reference sheet!
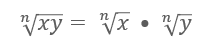
Understanding the Product Property of Radicals (Includes an example with real numbers!)
Analyzing a Perfect Square
Before we dive into analyzing any square roots, you will want to make sure that you know the perfect squares through 10 and some of the perfect cubes.
I've created a table of perfect square roots and cubes! Download this document and have it by your side as your study square roots and radicals.
Here we are asked to simplify the square root of 4.
You probably already know the answer to this problem, but let's break it down and think about how we come up with the answer.
We first have to think of "what number squared is 4?
That answer is 2, right? Let's write it like this:
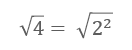
We know that anytime we take the square root of a number squared, our answer is that base number. So....
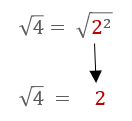
There are so many properties in math that allow us to solve problems. I'm going to introduce you to a property in Algebra called the "Product Property of Radicals".
But first, I want you to think about this...
If I have the number 6, is it okay to express this number as 3 times 2?
That works, right? Both sides of the equation are equal because 3 times 2 equals 6.
This property works the same way! Check it out!
Product Property of Radicals
**If n is even, then x and y must both be nonnegative**
So, I know these technical properties are difficult to understand. Let's take a look at this property using numbers.
Product Property of Radicals (Using Numbers)
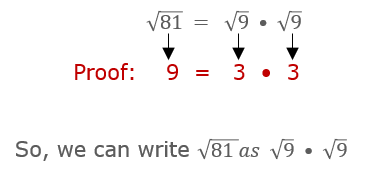
Now we are going to use this property and our knowledge of square and square roots to simplify a non-perfect square root!
Simplifying the Square Root of 18
Since 18 is not a perfect square, we must simplify this expression by rewriting it as a product of 2 square roots. We want to rewrite this so that one of the factors is a perfect square.
Let's first think of the factors for 18.
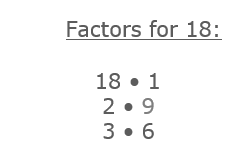
Now, we need to see if any of these factors are a perfect square.
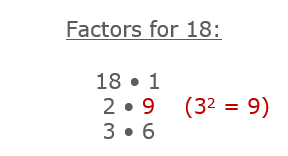
Since 9 is a perfect square, we will rewrite this square root using its factors of 9 and 2.
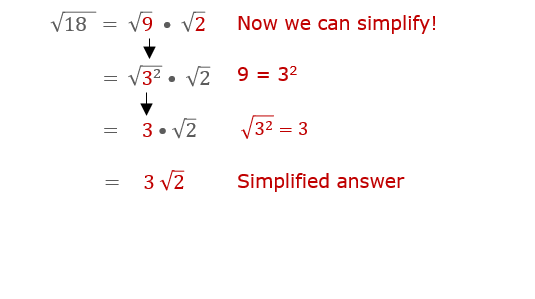
Did you notice how we rewrote the square root of 18 as the product of 2 factors, and one of them was a perfect square?
This allowed us to take the square root of the perfect square (which results in a whole number) and then we must leave the square root of 2, as the square root of 2 because it cannot be simplified any further.
Let's take a look at another example.
Simplifying the Negative Square Root of 125
Notice that 125 is not a perfect square, and there is a negative sign outside of the radical.
The negative sign outside of the radical means that our answer will be negative, but we don't really have to worry about that until the end.
Our first job is to think of the factors of 125. In particular, we want one of those factors to be a perfect square.
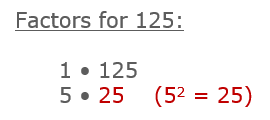
It works out perfect that the main factors for 125 is 5 and 25. 25 is a perfect square and this allows us to continue simplifying this square root!
Now we can rewrite the square root like this:
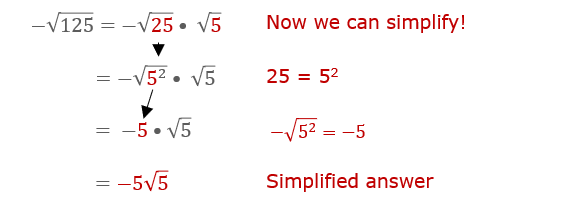
So, how are you doing? This isn't such a bad process when you think of simplifying in terms of perfect squares!
Let's take a look at one more example. This one is a little different!
Simplifying The Product of the Square Root of 8 and Square Root of 3
This problem is a little different in that it is written as a product of two square roots.
First we want to see if either one of the factors is a perfect square.
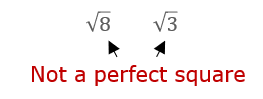
Unfortunately, 8 nor 3 are perfect squares, so we need to see if there is another way to simplify.
We know from the Product Property of Radicals that we can multiply 8 times 3 and write it as one square root, like this:

I hope this helps you to simplify square roots. We will continue simplifying square roots by simplifying square roots of algebraic expressions.

Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.


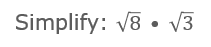





Comments
We would love to hear what you have to say about this page!