Translating Algebra Expressions

You've learned how to work with variables and how to evaluate algebra expressions, now we are going to translate words into algebraic expressions.

This skill will come in handy when working with word problems or real life situations. Pay close attention to the "key words" that represent mathematical operations.

You are probably very used to translating words into numerical expressions. Think about this...



We are used to seeing the words, plus, sum, difference, minus, product ...

The good news is that these very same words that we use to write numerical expressions are going to be used to write algebra expressions.

The difference between a numerical expression and an algebra expression is that we will be using variables when writing an algebraic expression. Instead of "8 plus 9" (with two given numbers), you would see, "a number plus 9".

We don't know exactly "what number", so we would use a variable to indicate that it can be any number.

Key words for each operation are indicated in bold. This will help you to easily translate the expression.


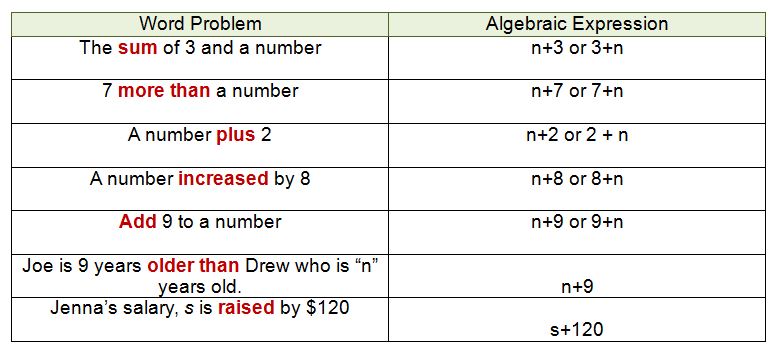
Algebraic Expressions and Key Words for Addition


As, you can see from the red, bold words, the key words for addition are: sum, more than, plus, increase, add, older than.

Please also remember that addition is commutative; therefore, you can reverse the digits and you will end up with the same answer.

Now, let's take a look at the key words for subtraction.


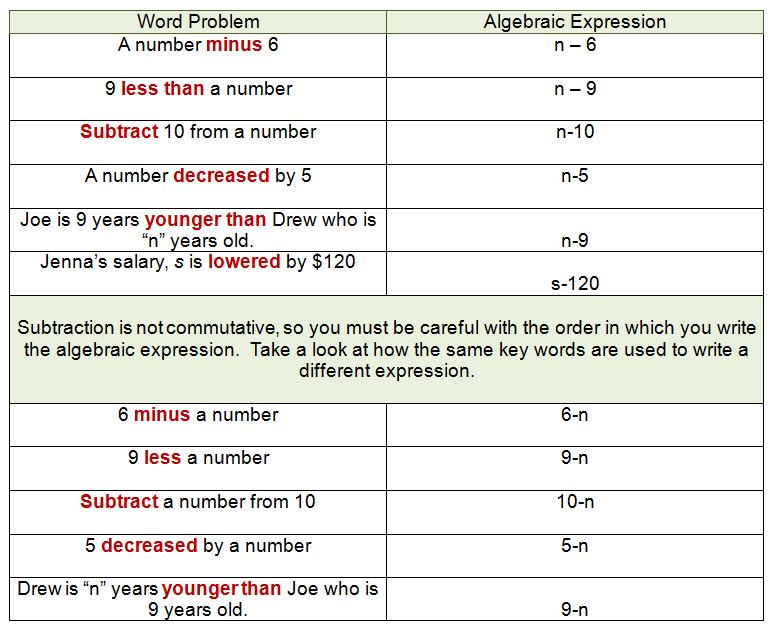
Algebraic Expressions and Key Words for Subtraction


Our key words for subtraction are: minus, less, subtract, decrease, younger than, and lowered. Remember that subtraction is not commutative, so the order in which write the digits does matter!

Now we'll take a look at key words for multiplication word problems.


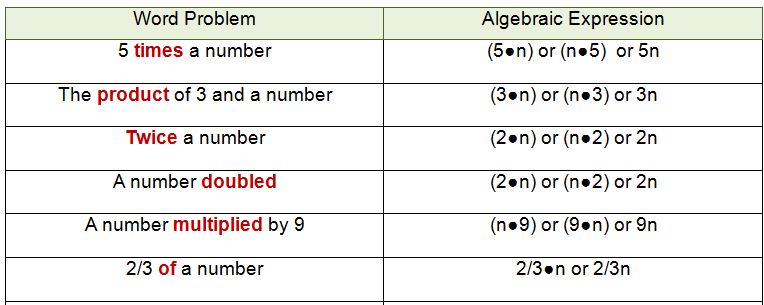
Algebraic Expressions and Key Words for Multiplication

The key words for multiplication are: times, product, twice, doubled, multiplied, and of. Of is the tricky word.

This is mostly used when you are multiplying a fraction times a number. For example 1/2 of a number means 1/2 times a number.

Think of "of" meaning to multiply when you are working with fractions.

The last operation that we will study is division. Division is not commutative, so you must pay close attention to the order in which you write the expression.


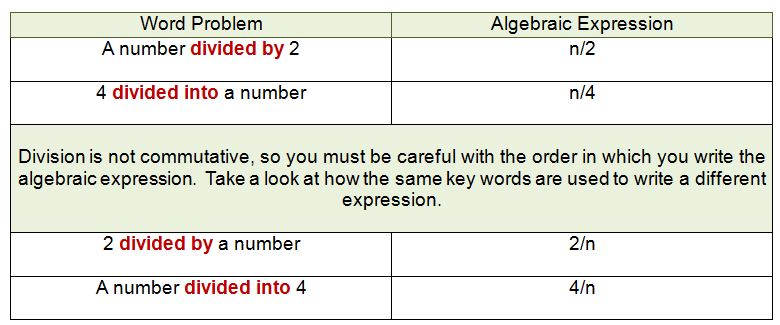
Algebraic Expressions and Key Words for Division

Division is much more simple. The key words are: divided by and divided into. Play close attention to the order in which it is written.

Quotient is also a key word for division. A quotient is the answer to a division problem.

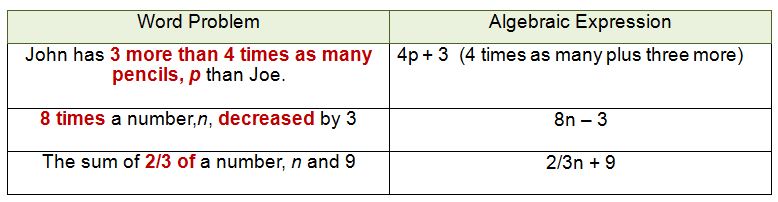
As you begin to work with algebraic expressions more, you will see word problems that require you to use more than one operation.

Take a look at these few examples:


Expressions with More Than One Operation


Many people struggle with translating word problems into algebraic expressions. This is a very brief lesson on simple algebraic expressions.

We will study this in more depth as we get into writing and solving algebraic word problems.

One of the most important things to remember is to look for key words and to make sure that your expression matches the context of the word problem.

This is most important for operations that are not commutative, such as subtraction and division.

The next lesson in this unit is on simplifying algebraic expressions.



  • Algebraic Expressions

    • Comments

    We would love to hear what you have to say about this page!

    Need More Help With Your Algebra Studies?

    Get access to hundreds of video examples and practice problems with your subscription! 

    Click here for more information on our affordable subscription options.

    Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.