Understanding Algebraic Variables

I'm sure you're wondering, "What is a variable and why are letters used in math?" If this hasn't crossed your mind, I'm sure it will as you begin your study of Pre-Algebra.

Understanding algebraic variables is the very first component for understanding Algebra. So, let's get started...


So, What is a Variable?

A variable is a symbol, most often a letter, that represents a number in math.

So, you say, "That's silly, why use a letter when you can just write the number? And... that's a very good question!

The term variable means "to change". This is the reason why we use algebraic variables. If a number can change based on the situation, then we would use a variable in it's place. This is better represented when we talk about formulas. Take a look....


Formulas and Algebraic Variables

Think about all of the math formulas that you have used in the past. I'm sure you are familiar with the area formula: A = lw or the perimeter formula: P= 2l+2w.

Notice how these formulas use variables. We use variables in our formulas because these numbers change based on what you are measuring.

Let's say that I'm calculating the money that I can make from my lawn service business. I might start by creating a chart:


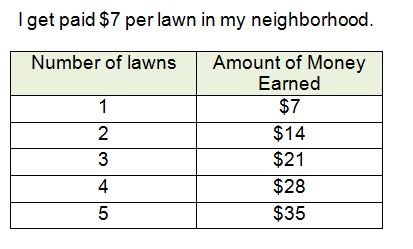
Since I multiply the number of lawns by $7 each time, I can write a formula (with a variable) to make this process easier.


Using Variables to Make Calculations Easier


In this way, I can always change "m" and substitute the number of lawns that I mowed that week and easily find my earnings.

Do you see how the variables, E and m change based on the number of lawns mowed? This is an easy way to calculate your earnings without the added work of a chart.



When working with variables, you must remember one thing:

No matter how many times a variable is used in an expression, the value is always the same.

For example take a look at the following expression: 2s + 6 - 3s

Notice how the variable "s" is used twice in this equation.

I CANNOT substitute two different numbers for "s". If s = 5, then 5 must be substituted for s in both places in the equation.

For example: 2s + 6 - 3s      where s = 5

This also means: 2(5)  + 6 - 3(5)

Notice how the number 5 takes the place of "s" in both places.


If you have two different variables in an expression, then most likely they will represent different values.

You will find that using variables in Algebra is actually an easy process. It will make some of the long labor intensive work in the past seem much easier!

This leads us right into our next lesson on evaluating algebraic expressions.



  • Algebraic Variables

    • Comments

    We would love to hear what you have to say about this page!

    Need More Help With Your Algebra Studies?

    Get access to hundreds of video examples and practice problems with your subscription! 

    Click here for more information on our affordable subscription options.

    Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.