Comparing Integers

As you begin your study of integers, you may feel a little confused, especially when working with negative integers.

We know that the negative integers are whole numbers that are less than 0. Since they are less than 0, they always lie to the left of 0 on the number line.

Positive integers are whole numbers greater than 0 and always lie to the right of 0 on the number line. These are the numbers that you've been working with since kindergarten, so you are now an expert.

Remember that 0 is neither negative or positive.

Let's take a look at our number line. If you use this number line to compare numbers, then the numbers increase as you move to the right and they decrease as you move to the left.



Now, let's order a set of integers using the number line.



Example 1 - Ordering Integers From Least to Greatest

Order the following set of numbers from least to greatest.

20, -5, 0, -2, 12, -18, 3, -11


Tip:

If you are asked to order integers from greatest to least, then you would order the numbers from the right of the number line to the left.

The greatest numbers are to the right of 0 and they decrease in value as you move to the left.


Using a number line makes ordering integers much easier and gives you a great visual if you have difficulty with this concept.

However, you may be asked to compare integers using the symbols, <, >, or =.

Let's quickly review the meaning of each of these symbols.


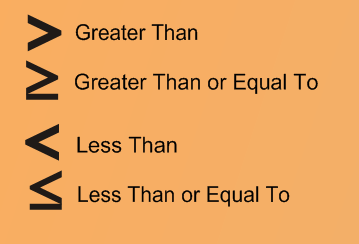
Now let's take a look at how we can use these symbols to compare integers.


Example 2 - Comparing Integers Using Inequality Symbols

Tips to Remember for Ordering or Comparing Integers

  • Positive numbers are always greater than negative numbers.

  • Negative numbers are always less than positive numbers

  • When using a number line, numbers increase as you move to the right

  • When using a number line, numbers decrease as you move to the left.

Hopefully you now have a better concept of positive and negative integers.

When in doubt, sketch a number line if you are having difficulty comparing or ordering integers.


  1. Home
    2. >
  2. Integers
    3. >
  3. Comparing Integers



Comments

We would love to hear what you have to say about this page!

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.