What is a Square Root?
As you progress through higher level math classes, you will come in contact with problems that contain square roots. The first question that is always asked is, "What is a square root?"
For many, this term is difficult to understand. Therefore, I'm going to show you a few different ways to think about square roots.
Understanding Squares
Before we can conquer square roots, we must first think about what it means to "square" a number. This will help you to better understand square roots.
When we "square" a number, we multiply the number by itself. For example:
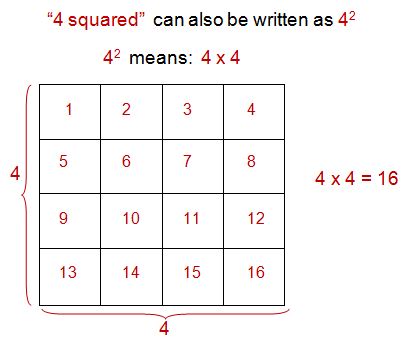
Notice how my illustration of 4x4 or "4 squared" created an actual square. This happened because we multiplied the number by itself. So there were the same number of rows as columns.
Any time you "square" a number, (which again means to multiply the number by itself) you will always end up with an array that is a perfect square.
Just to prove it to you, take a look at the following two models for 3 squared (32) and 2 squared (22).
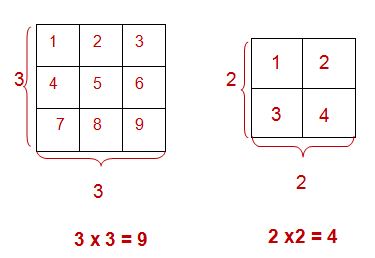
Notice again, how we created perfect squares since we were multiplying the number times itself.
Now.. Think About Opposites
Now let's switch gears and instead of "squaring a number" we are going to talk about "taking the square root".
The coolest thing about math is that there are a ton of opposites.
Think about it:
The opposite of add is subtract.
The opposite of multiply is divide.
Knowing that these operations were opposites made learning our basic facts much easier because of fact families and opposites!
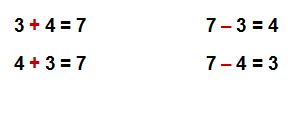
Since addition and subtraction are opposites, we could create a fact family with the numbers, 3, 4, and 7 and write four related facts.
So....Guess What?
Squaring a Number and Taking the Square Root are Opposites!
This will make square roots so much easier to understand because if they are opposites, then we can think of them as a family. So....

Just in case you forgot from our last lesson, Introduction to Radicals, the square root is written with a radical sign.

So, Here's How You Think of Square Roots...
When you see a square root problem, you want to think:
"What number could I square (or multiply by itself) to get this number?
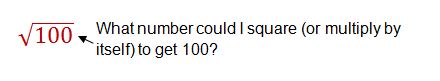
Let's take a look at a couple of examples...
Square Root Example 1
Let's start with our example above. Evaluate the square root of 100.
So think... "What number could I square (or multiply by itself) to get 100"?
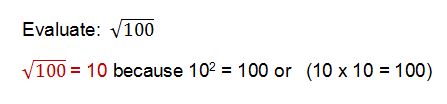
Since I knew that 10 squared equals 100, I know that the square root of 100 is 10.
Isn't it cool how opposites work in math?
Square Root Example 2
Let's look at one more example. Evaluate the square root of 144.
So think... "What number can I square (or multiply by itself) to get 144?"
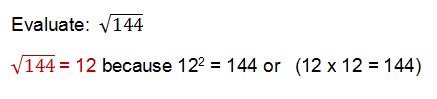
Since I knew that 12 squared equals 144, I know that the square root of 144 is 12.
The Beauty of "Perfect" Squares
All of our above examples are what we call "Perfect Squares". That means that when you take the square root, you get a whole number as your answer.
Not all square roots are "perfect squares". But take a minute to look at a few perfect squares that you should memorize.

This is just the beginning of square roots. In the following lessons, you will learn how to simplify non-perfect square roots, add and subtract square roots, and multiply and divide square roots.
Yes, the fun is just beginning, so hang in there!
I hope this lesson helps get you started. Please follow along below for more fun with square roots!
- Home >
- Radicals >
- Square Roots

Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.





Comments
We would love to hear what you have to say about this page!