Writing Algebra Equations
Finding the Equation of a Line Given Two Points

We have written the equation of a line in slope intercept form and standard form. We have also written the equation of a line when given slope and a point. Now we are going to take it one step further and write the equation of a line when we are only given two points that are on that line.

This type of problem requires three steps.

Example 1: Writing an Equation Given Two Points

Write an equation for the line that passes through the points (1,6) and (3,-4).

We know that we are given two points. Let's use a chart to help us organize our information.

In the chart below, notice that the slope and y-intercept are grey. These are the two values that must know to write an equation in slope intercept form.

We know that if we have two points, we can use the slope formula to find the slope.

Now we know the slope and we just need to find the y-intercept.  If we know the slope and 1 point, we can find the y-intercept.

Step 3: Write the equation in slope intercept form.

Slope (m) = -5

Y-intercept (b) = 11

y = mx + b

y = -5x + 11

Let's quickly review the steps for writing an equation given two points:

1. Find the slope using the slope formula.

2. Find the y-intercept by substituting the slope and the coordinates of 1 point into the slope intercept formula, y = mx + b.

3. Write the equation using the slope and y-intercept.

Ok, now let's apply this skill to solve real world problems. Now you will have to read through the problem and determine which information gives you two points. Remember a point is two numbers that are related in some way.

NOTE: Also remember, that when identifying a point from a word problem, "time" is always the x-coordinate.

Example 2: Solving a Real World Problem Given Two Points

The mathematics department sponsors Math Family Fun Night every year. In the first year, there were 35 participants. In the third year there were 57 participants.

• Write an equation that can be used to predict the amount of participants, y, for any given year, x.
• Based on your equation, how many participants are predicted for the fifth year?
  

Step 1: Identify your two points.

Let x = the year

Let y = number of participants

We know that the first year, there were 35 participants. This can be written as (1,35)

In the third year, there were 57 participants. This can be written as (3,57).

Therefore, our two points are (1,35) and (3,57)

Let's enter this information into our chart.

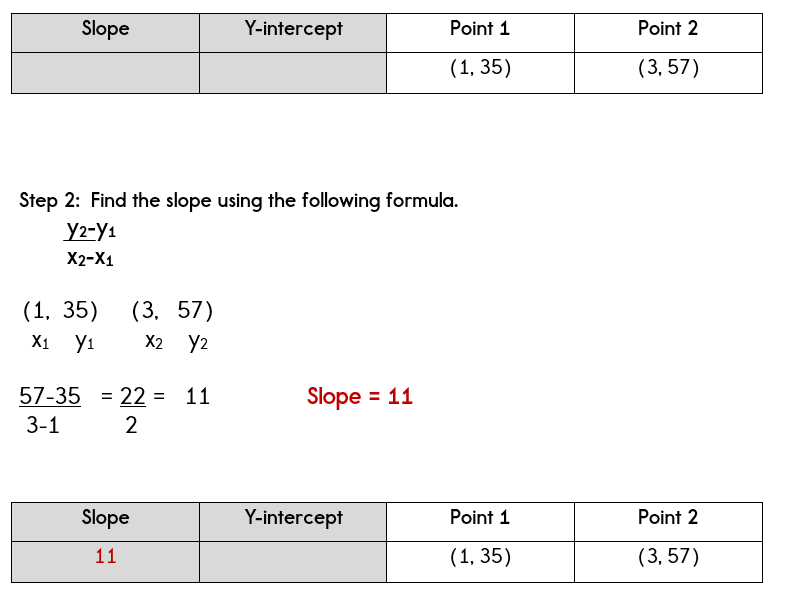
Now that we have an equation, we can use this equation to determine how many participants are predicted for the 5th year.

All we need to do is substitute!

We will substitute 5 for x (x is the year) and solve for y.

y = 11x + 24

y = 11(5) + 24

y = 55 + 24

y = 79

There are 79 participants predicted for the 5th year.

And that's it! Not too bad, is it? I hope that you are learning how to recognize points, slope and y-intercepts when reading real world problems.

You may also want to visit our lesson on writing equations using point-slope form.

1. Home
>
2. Writing Equations
>
3. Writing Equations Given Two Points

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.

Copyright © 2009-2020   |   Karin Hutchinson   |   ALL RIGHTS RESERVED.