Equivalent Fractions
At the end of this lesson, you will be able to identify equivalent fractions (or equal fractions).
Before we begin, let's first do a quick review of the vocabulary associated with fractions.
Why are Fractions used to represent numbers that are part of a whole?
A fraction indicates a number that is less than a whole. Fractions are easier to understand by looking at a graphic. Take a look....
When you cut an orange in 1/2, you no longer have a whole orange. Each piece is only part of the whole orange.
This represents the fraction 1/2.
When you eat a piece of pie, you are eating a "part" of the pie.
This is also called a "fraction" of the pie.
Fractions that are Equivalent
Now let's take a look at fractions that are equivalent.
Equivalent means "equal". Therefore, equivalent fractions are fractions that are equal in value.
Take a look at the following picture which shows three different fractions, that are all worth exactly the same amount.
Let's pretend these are one of those large Hershey bars.
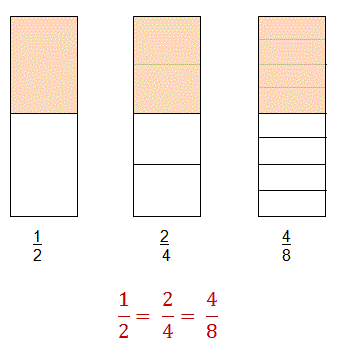
As you can see from the picture above, if you eat 1/2 of the hershey bar, you will eat the same amount if you eat 2/4 of the hershey bar.
You can also eat 4/8 and you would have eaten the same amount.
These 3 fractions are equal or equivalent.
Writing Equivalent Fractions
Now that you know what equal fractions look like, let's explore how we can write fractions that are equivalent.
We'll first take a look at the fractions we used with our Hershey Bar example above.
This leads us into the Equal Fractions Property.
Equal Fractions Property
If the numerator and denominator of a fraction are multiplied (or divided) by the same nonzero number, then the resulting fraction is equivalent to the original fraction.
Let's put this property into action! Take a look at example 1.
Example 1 - Equivalent Fractions
Not too bad, is it? Yes, I know fractions are intimidating, but think about what you are doing and why it makes sense.
In this lesson, in order to identify fractions that are equivalent, you must multiply the numerator and denominator by the same number.
Why the same number? When you multiply the numerator and denominator by the same number, you are actually multiplying by 1.
Think about it: 2/2 = 1 and 5/5 = 1 and 20/20 = 1
When you multiply by 1, you get "the same answer". This is the reason why we are able to identify equivalent or equal fractions.
With this quick refresher, you are now able to move onto the next lesson which is on simplifying fractions.
Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.
Need Help? Try This Online Calculator!
Affiliate Products...
On this site, I recommend only one product that I use and love and that is Mathway If you make a purchase on this site, I may receive a small commission at no cost to you.
Comments
We would love to hear what you have to say about this page!