Graphing Systems of Inequalities
Practice Problems

How did you like the Systems of Inequalities examples? Did the color coding help you to identify the area of the graph that contained solutions? I hope so!

In order to complete these practice problems, you will need graph paper, colored pencils or crayons, and a ruler. If you don't have colored pencils or crayons, that's ok. You can draw horizontal lines for one graph and vertical lines for another graph to help identify the area that contains solutions.


Let's quickly review our steps for graphing a system of inequalities.


Systems of Inequalities

  • Graph the first inequality. (Pay attention to your boundary line and make sure you shade the half plane that contains the solutions to the inequality.)

  • Graph the second inequality on the same graph. (Shade the correct half plane in a different color or use a different design with your pencil.)

  • Identify the area that is shaded by BOTH inequalities. This is the solution to the system of inequalities.

Are you ready to practice a few on your own? Let's do it!


Practice Problems

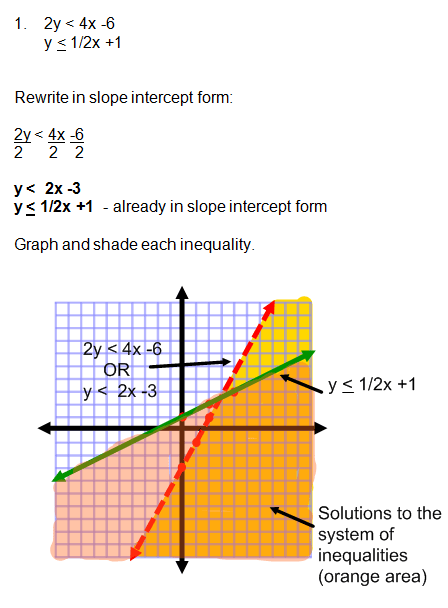
1.  2y < 4x - 6 and y < 1/2x + 1

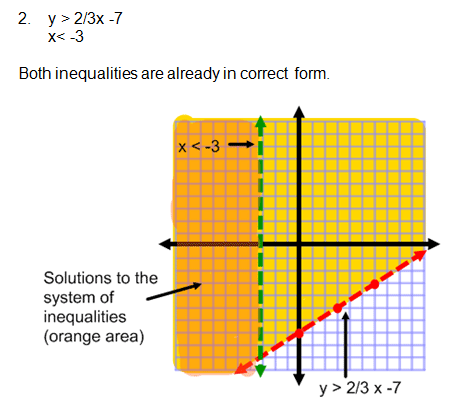
2.  y > 2/3x - 7 and x < -3

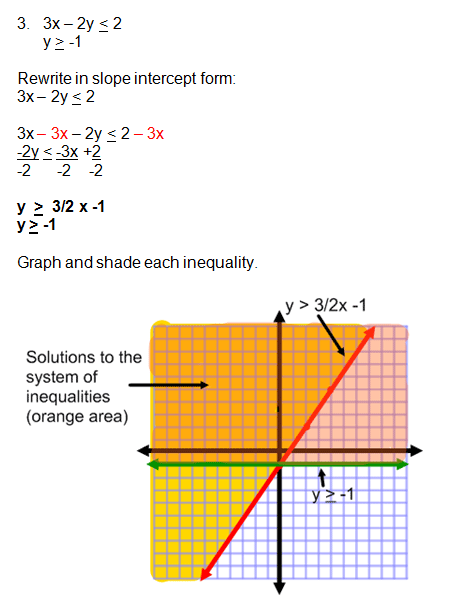
3.  3x - 2y < 2 and y > -1


Now it's time to check your answers. Pay special attention to the boundary lines and the shaded areas.


Solutions

This first problem was a little tricky because you had to first rewrite the first inequality in slope intercept form. Dividing all terms by 2, was your first step in order to be able to graph the first inequality.

Systems of Inequalities example


Now let's take a look at your graph for problem 2. This problem was a little tricky because inequality number 2 was a vertical line.

Problem 2

Graphing systems of inequalities example 2


Problem 3 is also a little tricky because the first inequality is written in standard form. The easiest way to graph this inequality is to rewrite it in slope intercept form.

SPECIAL NOTE: Remember to reverse the inequality symbol when you multply or divide by a negative number!


Problem 3

Graphing systems of inequalities


  1. Home
    2. >
  2. Inequalities
    3. >
  3. Systems of Inequalities
    4. >
  4. Practice Problems



Comments

We would love to hear what you have to say about this page!

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.