Dividing Monomials
How Do We Divide When Exponents are Involved?
As you've seen in the prior lessons, when we work with monomials, we see a lot of exponents.
You've discovered the laws of exponents and the properties for multiplying exponents, but what happens when we divide? That is the question we are going to answer in this lesson.
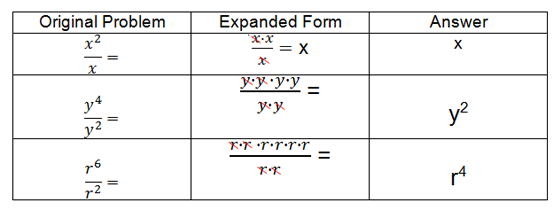
Let's start by taking a look at a few problems in "expanded form". Once you examine these examples, you'll discover the rule on your own.
Expanded Form Examples
Take a look at the exponents in the original problem and then analyze the exponents in the answer for each example.
Can you figure out the rule for exponents when you are dividing?
Dividing Monomials
When you divide powers that have the same base, you subtract the exponents.
That's a pretty easy rule to remember! It's the opposite of the multiplication rule.
When you multiply powers that have the same base, you add the exponents and when you divide powers that have the same base, you subtract the exponents.
Let's look at a couple of examples.
Example 1: Dividing Monomials
And.... another example.
Example 2

That's a pretty easy rule to remember! Let's take a look at one more property. This property is called, Power of a Quotient Property.
So, what is a quotient?
Quotient
A Quotient is an answer to a division problem.
Let's take a look at what happens when you raise a fraction (or a division problem) to a power.
Remember: A division bar and fraction bar are synonymous!
Power of a Quotient Property
To find the power of a quotient, raise the numerator to the power, and the denominator to the power. Then divide.
Let's take a look at a few examples.
Power of a Quotient: Example 1
Power of a Quotient: Example 2

You may now be ready to move onto the next lesson which is simplifying monomials.

Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.
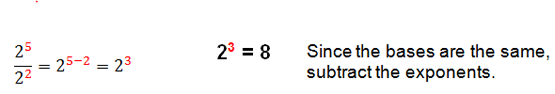
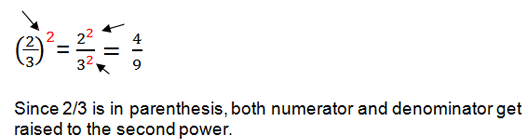





Comments
We would love to hear what you have to say about this page!