Finding the Least Common Multiple

If you've ever added or subtracted fractions, then you've found the least common multiple (LCM) of 2 numbers.

You may not have called it the "least common multiple", instead you may have called it the "least common denominator", but it's all the same.

If you haven't gotten this far in your study of fractions, it's ok.

You'll learn how to identify the LCM and apply it when working with fractions. Let's first take a look at a few definitions.

Our first definition is the term multiple.

The multiple of a number is the product of the number and any nonzero whole number. (Remember: a product is the answer to a multiplication problem).

So, take a look at the following example of a multiple.

A common multiple is a multiple that is shared by 2 or more numbers. Let's take a look...


This leads us to our current vocabulary word: least common multiple.

The least of the common multiples of two or more numbers is called the least common multiple or LCM. Take a look at the following example.


You can also find the least common multiple by using prime factorization. This can be helpful for larger numbers.


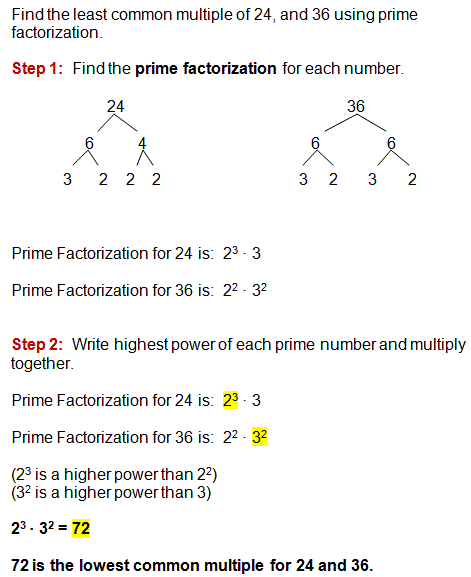
You will see as you begin to add and subtract fractions, that finding the least common multiple will become second nature.

You will also use the least common multiple as you compare fractions in the next lesson.



  1. Home
    2. >
  2. Fractions
    3. >
  3. LCM



Comments

We would love to hear what you have to say about this page!

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.