Scientific Notation

Since we've done so much work with exponents, we are going to continue our studies by looking at scientific notation.

Scientific notation is simply a "shorter way" of writing very large or very small numbers.

Scientists often work with very large or extremely small numbers when performing experiments, which is why it is called "scientific" notation.

There is a specific format in which you must write a number in order for it to be considered scientific notation. Let's take a look:

It's really important that you understand the format for scientific notation, so let's look at a chart that illustrates a few incorrect and correct ways to write numerals in scientific notation.

Are you wondering why we have to multiply by 10 to a power? Why 10 and not 5 or 3? Let's investigate.

First, let's investigate the powers of 10.  Do you know your powers of 10?

10¹ = 10

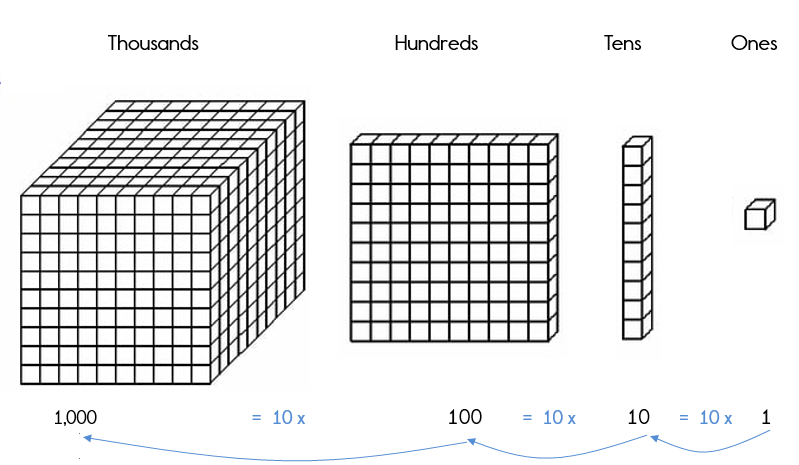
10¹ = 10

10² = 10 x 10 = 100

10³ = 10 x10 x 10 = 1,000

10⁴ = 10 x10 x10 x10 = 10,000

10⁵ = 10 x10 x 10 x 10 x 10 = 100,000

Notice how when we multiply by 10, it makes the product ten times greater.
Now let's apply this to scientific notation.

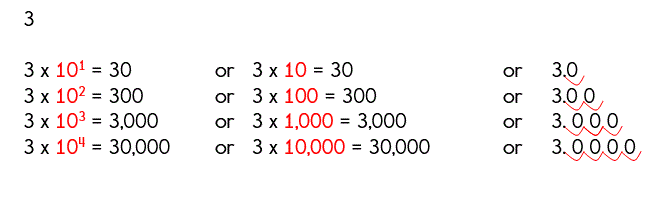
Do you see the pattern? We continue to move another place value to the right when we multiply by 10.

Notice that the three itself remains unchanged. We just continue to move the decimal point a certain number of spaces to the right depending on the power of 10 that we are multiplying.

For example, if I multiply by 10³, then I will move the decimal point 3 places to the right. This is equivalent to multiplying by 1000.

Let's take a look at a couple of examples of numbers written in scientific notation and rewrite them in expanded form.

Example 1: Write in Expanded Form

---

Example 2: Adding the Decimal Point

---

Now, let's look at a few examples in expanded form and rewrite them in scientific notation.

Example 3: Write in Scientific Notation

---

So, how are you feeling about scientific notation when the power of 10 is positive? It gets easier as you practice a little more, I promise!

Are you ready to look at a few problems where the power of 10 is negative? Don't worry - same process, we're just going to move the decimal in a different direction!

If you studied the lesson on negative exponents, then you learned that when you raise a whole number to a negative power, it results in a fraction because you take the recipocal.

And... we all know that proper fractions have a smaller value than whole numbers. So, when we work with powers of 10 to a negative power, we are going to be working with very small numbers.

Let's take a look at a couple of examples written in scientific notation and expand them.

Example 4: Write in Expanded Form

---

Example 5: Adding the Decimal Point

---

Let's look at one more example. I've given you the expanded form this time, and would like to show you how to write it in scientific notation.

Pay special attention to where I stop counting when I move my decimal to the right.

Example 6: Scientific Notation

---

Awesome Job! In the next lesson, we'll take a look at more difficult problems involving scientific notation! See you there!

1. Home
>
2. Exponents
>
3. Scientific Notation

---

---

Copyright © 2009-2020   |   Karin Hutchinson   |   ALL RIGHTS RESERVED.