Negative Exponents and Zero Exponents

So far in this unit, you've learned how to simplify monomial expressions with positive exponents. Now we are going to study two more aspects of monomials: those that have negative exponents and those that have zero as an exponent.

I am going to let you investigate to see if you can come up with the rule on your own! Take a look at the following problems and see if you can determine the pattern.

Negative exponents

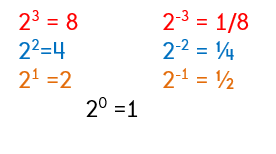
Can you figure out the rule? If not, here it is...


The Rule for Negative Exponents:

The expression a-n is the reciprocal of an

TIP:

A reciprocal is when you "flip a fraction".

Examples:

The reciprocal of 3/4 is 4/3.

The reciprocal of 5 is 1/5. (You can make a whole number a fraction by putting a one in the denominator: 5 = 5/1)

***An easy rule to remember is: if the number is in the numerator (top), move it to the denominator (bottom). If the number is in the denominator, move it to the numerator!


Let's take a look at a couple of examples:


Examples of Negative Exponents

Examples of negative exponents

Now let's quickly take a look at monomials that contain the exponent 0.


Any number (except 0) to the zero power is equal to 1.

Monomials with an exponent of 0


Not too hard, is it? Let's look at a couple of example problems and then you can practice a few.


Example 1: Negative Exponents

Monomial expression with a negative exponent




Example 2: Evaluating Negative Exponents

Evaluating negative exponents

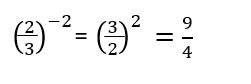
**Since 2/3 is in parenthesis, we must apply the power of a quotient property and raise both the 2 and 3 to the negative 2 power.

First take the reciprocal to get rid of the negative exponent.

Then raise (3/2) to the second power.



Now, it's going to get a little more tough.



Example 3: Complex Expressions with Negative Exponents

Complex expressions with negative exponents

One more example.


Example 4: More Negative Exponents

Simplifying expressions with negative exponents

Yes, I know that's a lot of examples to comprehend. My goal was to start easy and progress to harder problems. Are you ready to try a few on your own?


Practice Problems

Negative exponent practice problems


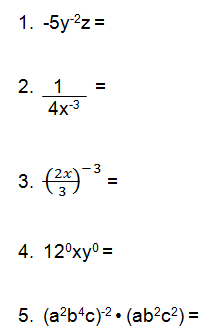
Solutions

Negative exponents
Solutions to negative exponents example

So, how did you do? Are you ready to move onto Scientific Notation?


  1. Home
    2. >
  2. Exponents
    3. >
  3. Negative Exponents



Comments

We would love to hear what you have to say about this page!

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.