Factor Trees - Using Prime Factorization to Identify the GCF

You've probably heard or learned about prime factorization (factor trees) in your basic math classes.

You probably don't use this on a daily basis, therefore, you may not remember how to find the prime factorization or you may not remember why it is used.

Let's start by defining a prime number.


Prime Number

A prime number is a positive integer, greater than 1, whose only factors are 1 and itself.

Prime numbers can be used to find the greatest common factor for a set of numbers.

I know you are still wondering WHY and HOW! Let's say you need to find the greatest common factor for the numbers 175 and 250.

Since these numbers are a little larger, identifying the common factors is not quite as easy.

This is where prime factorization may be a little faster. Many people also call prime factorization the process of making a factor tree.

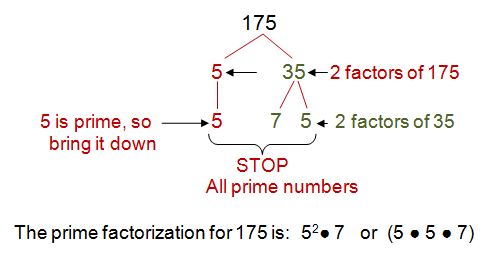
First I'm going to make a factor tree for 175. Take a look....


Example 1 - Using Factor Trees to Find the GCF

Part 1 - Prime Factorization for 175

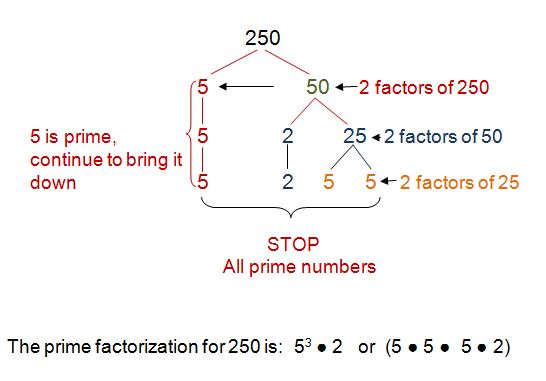
Prime Factorization for 175


Prime Factorization for 250

Prime factorization for 250


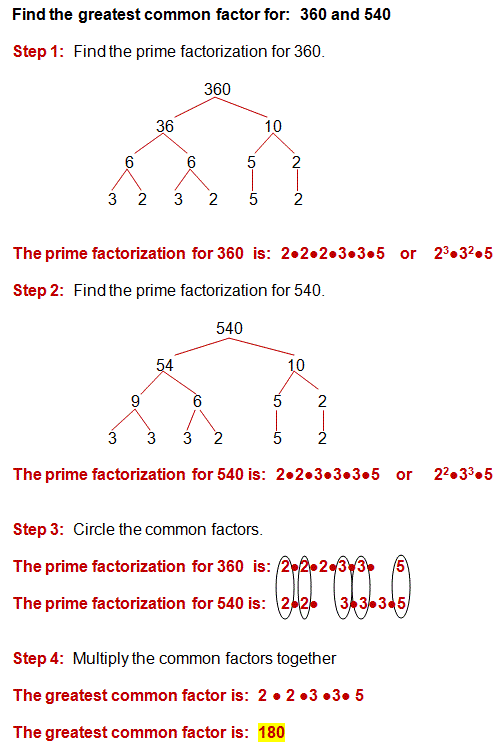
Greatest Common Factor for 175 & 250

Now that we know the prime factorization for 175 and 250, we can identify the greatest common factor.

Using Prime Factorization to find the GCF


Yes, it looks like a long complicated process, but it's not too bad.

It does require a little more writing, but if you are working with larger numbers, prime factorization is the fastest way to identify the greatest common factor.

This first example is thoroughly explained and labeled, in order to make sure that you understand the process.

Let's look at one more example, without as many labels, so that you can see how this process should look on your paper.


Example 2

Using Factor Trees to find the GCF


Factor trees (or prime factorization) can be an easy way to find the greatest common factor for two large numbers.

Simply find all of the prime factors and identify the common factors.

Multiply your common factors together and you end up with the greatest common factor for both numbers!

Now that you know two ways to find the greatest common factor of two numbers, you are ready for the next lesson on equivalent fractions.


  1. Home
    2. >
  2. Fractions
    3. >
  3. Prime Factorization



Comments

We would love to hear what you have to say about this page!

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.